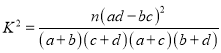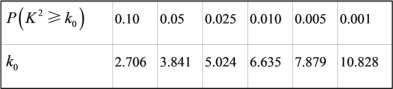题目内容
【题目】已知抛物线![]() 和点
和点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于另一点
交于另一点![]() .给出以下判断:
.给出以下判断:
①直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() ;
;
②![]() 轴;
轴;
③以![]() 为直径的圆与抛物线准线相切.
为直径的圆与抛物线准线相切.
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
【答案】B
【解析】
由题意,可设直线![]() 的方程为
的方程为![]() ,利用韦达定理判断第一个结论;将
,利用韦达定理判断第一个结论;将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,进而判断第二个结论;设
,进而判断第二个结论;设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,则圆心
,则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,进而判断第三个结论.
三点不共线,进而判断第三个结论.
解:由题意,可设直线![]() 的方程为
的方程为![]() ,
,
代入抛物线![]() 的方程,有
的方程,有![]() .
.
设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所![]() .
.
则直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() .所以①正确.
.所以①正确.
将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,
,
根据抛物线的对称性可知,![]() ,
,![]() 两点关于
两点关于![]() 轴对称,
轴对称,
所以直线![]() 轴.所以②正确.
轴.所以②正确.
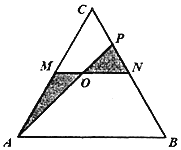
如图,设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,
,
则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,
则![]() .所以③不正确.
.所以③不正确.
故选:B.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案【题目】某校高三课外兴趣小组为了了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
附:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
![]()
![]()