题目内容
实数x,y满足
,则u=
的范围是
|
| y+2 |
| x-2 |
(-∞,-4]∪[2,+∞)
(-∞,-4]∪[2,+∞)
.分析:不等式组
,表示一个三角形区域(包含边界),三角形的三个顶点的坐标分别为A(1,2),B(4,2),C(3,1),u=
的几何意义是点(x,y)与P(2,-2)连线的斜率,求出PA,PB的斜率,即可得到结论.
|
| y+2 |
| x-2 |
解答: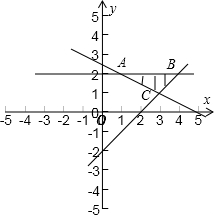 解:不等式组
解:不等式组
,表示一个三角形区域(包含边界),三角形的三个顶点的坐标分别为A(1,2),B(4,2),C(3,1)
u=
的几何意义是点(x,y)与P(2,-2)连线的斜率,由于kPA=
=-4,kPB=
=2
∴u=
的范围是(-∞,-4]∪[2,+∞)
故答案为:(-∞,-4]∪[2,+∞)
 解:不等式组
解:不等式组
|
u=
| y+2 |
| x-2 |
| 2+2 |
| 1-2 |
| 2+2 |
| 4-2 |
∴u=
| y+2 |
| x-2 |
故答案为:(-∞,-4]∪[2,+∞)
点评:本题考查线性规划知识,考查斜率的定义,解题的关键是确定平面区域,理解目标函数的几何意义.

练习册系列答案
相关题目
设实数x,y满足
,则 u=
-
的取值范围为( )
|
| y |
| x |
| x |
| y |
A、[
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|