题目内容
(1)已知矩阵M 所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.
所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.(2)已知直线l:3x+4y-12=0与圆C:
 (θ为参数 )试判断他们的公共点个数;
(θ为参数 )试判断他们的公共点个数;(3)解不等式|2x-1|<|x|+1.
【答案】分析:(1)由矩阵的线性变换列出关于x和y的一元二次方程组,求出方程组的解集即可得到点A的坐标;可设出矩阵M的逆矩阵,根据逆矩阵的定义得到逆矩阵与矩阵M的乘积等于单位矩阵,得到一个一元二次方程组,求出方程组的解集即可得到M的逆矩阵;
(2)把圆的参数方程化为普通方程后,找出圆心坐标与半径,然后利用点到直线的距离公式求出圆心到直线的距离d与半径r比较大小得到直线与圆的位置关系,即可得到交点的个数;
(3)分三种情况x大于等于 ,x大于等于0小于
,x大于等于0小于 和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可.
和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可.
解答:解:(1)由题意可知 (x,y)=(13,5),即
(x,y)=(13,5),即 ,
,
解得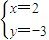 ,所以A(2,-3);
,所以A(2,-3);
设矩阵M的逆矩阵为 ,则
,则 •
• =
= ,即
,即 ,
,
且 ,解得a=-1,b=3,c=-1,d=2
,解得a=-1,b=3,c=-1,d=2
所以矩阵M的逆矩阵为 ;
;
(2)把圆的参数方程化为普通方程得(x+1)2+(y-2)2=4,圆心(-1,2),半径r=2
则圆心到已知直线的距离d= =
= <2=r,得到直线与圆的位置关系是相交,
<2=r,得到直线与圆的位置关系是相交,
所以直线与圆的公共点有两个;
(3)当x≥ 时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[
时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[ ,2);
,2);
当0≤x< 时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0,
时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0, );
);
当x<0时,原不等式变为:1-2x<-x+1,解得x>0,所以原不等式无解.
综上,原不等式的解集为[0,2).
点评:此题考查学生会求矩阵的逆矩阵及掌握矩阵的线性变换,灵活运用点到直线的距离公式化简求值,掌握直线与圆的位置关系的判断方法,会利用讨论的方法求绝对值不等式的解集,是一道综合题.
(2)把圆的参数方程化为普通方程后,找出圆心坐标与半径,然后利用点到直线的距离公式求出圆心到直线的距离d与半径r比较大小得到直线与圆的位置关系,即可得到交点的个数;
(3)分三种情况x大于等于
 ,x大于等于0小于
,x大于等于0小于 和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可.
和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可.解答:解:(1)由题意可知
 (x,y)=(13,5),即
(x,y)=(13,5),即 ,
,解得
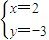 ,所以A(2,-3);
,所以A(2,-3);设矩阵M的逆矩阵为
 ,则
,则 •
• =
= ,即
,即 ,
,且
 ,解得a=-1,b=3,c=-1,d=2
,解得a=-1,b=3,c=-1,d=2所以矩阵M的逆矩阵为
 ;
;(2)把圆的参数方程化为普通方程得(x+1)2+(y-2)2=4,圆心(-1,2),半径r=2
则圆心到已知直线的距离d=
 =
= <2=r,得到直线与圆的位置关系是相交,
<2=r,得到直线与圆的位置关系是相交,所以直线与圆的公共点有两个;
(3)当x≥
 时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[
时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[ ,2);
,2);当0≤x<
 时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0,
时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0, );
);当x<0时,原不等式变为:1-2x<-x+1,解得x>0,所以原不等式无解.
综上,原不等式的解集为[0,2).
点评:此题考查学生会求矩阵的逆矩阵及掌握矩阵的线性变换,灵活运用点到直线的距离公式化简求值,掌握直线与圆的位置关系的判断方法,会利用讨论的方法求绝对值不等式的解集,是一道综合题.

练习册系列答案
相关题目
 ,N=
,N= ,且MN=
,且MN= 。
。 =2
=2 sin
sin 。
。 3的解集为
3的解集为 ,求实数a的值;
,求实数a的值; ,
, ,且
,且 ,
, (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ,
, ,
, ,且
,且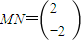 ,
,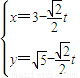 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ,
,