题目内容
本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.(1)已知矩阵M=
 ,
, ,且
,且 ,
,(Ⅰ)求实数a,b,c,d的值;(Ⅱ)求直线y=3x在矩阵M所对应的线性变换下的像的方程.
(2)在直角坐标系xoy中,直线l的参数方程为
 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
.(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线l交于点A、B,若点P的坐标为
 ,
,求|PA|+|PB|.
(3)已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
【答案】分析:选作题1:(Ⅰ)由矩阵MN的表达式,把他们相乘使左边等于右边既可求解实数a,b,c,d的值.
(Ⅱ)矩阵M所对应的线性变换将直线变成直线,可选直线y=3x上的两点做矩阵M所对应的线性变换下的像,即可确定原直线的像.
选做题2:(Ⅰ)由极坐标转化为直线坐标方程.
(Ⅱ)将直线的参数方程代入圆的直角坐标系,根据根与系数关系求出两实根的关系式,再有t的几何意义求解.
选做题3:(Ⅰ)首先把函数的参数表达式≤3,解不等式求出a的值.
(Ⅱ)由上题解得的当a=2时,f(x)=|x-2|,可设函数g(x)=f(x)+f(x+5),求出g(x)的函数表达式使其≥m对一切实数x恒成立.求解M的范围.
解答:(1)选修1:解:(Ⅰ)由题设得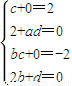 ,解得
,解得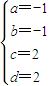 ;
;
(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线y=3x上的两(0,0),(1,3),
由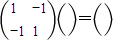 ,
,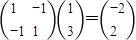 ,
,
得点(0,0),(1,3)在矩阵M所对应的变换下的线的像是(0,0),(-2,2),
从而直线y=3x在矩阵M所对应的线性变换下的像的方程为y=-x.
(2)选修2:解:(Ⅰ)由ρ=2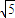 sinθ得x2+y2-2
sinθ得x2+y2-2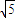 y=0,即
y=0,即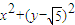 =5.
=5.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得 =5,
=5,
即t2-3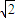 t+4=0,
t+4=0,
由于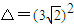 -4×4=2>0,
-4×4=2>0,
故可设t1,t2是上述方程的两实根,
所以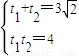 ,
,
又直线l过点P(3,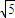 ),
),
故由上式及t的几何意义得:
|PA|+|PB|=|t1|+|t2|=t1+t2=3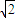 .
.
(3)选修3:解:(Ⅰ)由f(x)≤3得|x-a|≤3,解得a-3≤x≤a+3,
又已知不等式f(x)≤3的解集为{x|-1≤x≤5},
所以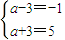 ,解得a=2.
,解得a=2.
(Ⅱ)当a=2时,f(x)=|x-2|,
设g(x)=f(x)+f(x+5),
于是g(x)=|x-2|+|x+3|=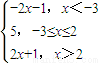 ,
,
所以,当x<-3时,g(x)>5;
当-3≤x≤2时,g(x)>5;
当x>2时,g(x)>5.
点评:选作题1主要考查矩阵与变换等基础知识,考查运算求解能力.计算量小属于较容易的题.
选作题2主要考查坐标系与参数方程的关系,考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力.较复杂.
选修3:本小题涉及不等式,主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力.较复杂.
(Ⅱ)矩阵M所对应的线性变换将直线变成直线,可选直线y=3x上的两点做矩阵M所对应的线性变换下的像,即可确定原直线的像.
选做题2:(Ⅰ)由极坐标转化为直线坐标方程.
(Ⅱ)将直线的参数方程代入圆的直角坐标系,根据根与系数关系求出两实根的关系式,再有t的几何意义求解.
选做题3:(Ⅰ)首先把函数的参数表达式≤3,解不等式求出a的值.
(Ⅱ)由上题解得的当a=2时,f(x)=|x-2|,可设函数g(x)=f(x)+f(x+5),求出g(x)的函数表达式使其≥m对一切实数x恒成立.求解M的范围.
解答:(1)选修1:解:(Ⅰ)由题设得
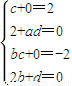 ,解得
,解得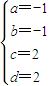 ;
;(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线y=3x上的两(0,0),(1,3),
由
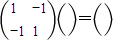 ,
,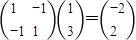 ,
,得点(0,0),(1,3)在矩阵M所对应的变换下的线的像是(0,0),(-2,2),
从而直线y=3x在矩阵M所对应的线性变换下的像的方程为y=-x.
(2)选修2:解:(Ⅰ)由ρ=2
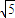 sinθ得x2+y2-2
sinθ得x2+y2-2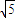 y=0,即
y=0,即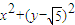 =5.
=5.(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得
 =5,
=5,即t2-3
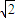 t+4=0,
t+4=0,由于
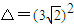 -4×4=2>0,
-4×4=2>0,故可设t1,t2是上述方程的两实根,
所以
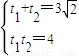 ,
,又直线l过点P(3,
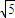 ),
),故由上式及t的几何意义得:
|PA|+|PB|=|t1|+|t2|=t1+t2=3
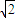 .
.(3)选修3:解:(Ⅰ)由f(x)≤3得|x-a|≤3,解得a-3≤x≤a+3,
又已知不等式f(x)≤3的解集为{x|-1≤x≤5},
所以
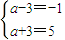 ,解得a=2.
,解得a=2.(Ⅱ)当a=2时,f(x)=|x-2|,
设g(x)=f(x)+f(x+5),
于是g(x)=|x-2|+|x+3|=
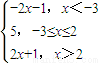 ,
,所以,当x<-3时,g(x)>5;
当-3≤x≤2时,g(x)>5;
当x>2时,g(x)>5.
点评:选作题1主要考查矩阵与变换等基础知识,考查运算求解能力.计算量小属于较容易的题.
选作题2主要考查坐标系与参数方程的关系,考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力.较复杂.
选修3:本小题涉及不等式,主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力.较复杂.

练习册系列答案
相关题目
 ,N=
,N= ,且MN=
,且MN= 。
。 =2
=2 sin
sin 。
。 3的解集为
3的解集为 ,求实数a的值;
,求实数a的值;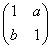 ,
,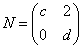 ,且
,且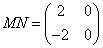 ,
,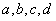 的值;(Ⅱ)求直线
的值;(Ⅱ)求直线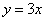 在矩阵M所对应的线性变换下的像的方程。
在矩阵M所对应的线性变换下的像的方程。 的参数方程为
的参数方程为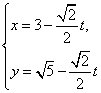 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为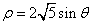 。
。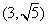 ,
,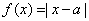 。
。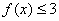 的解集为
的解集为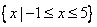 ,求实数
,求实数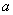 的值;
的值;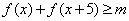 对一切实数x恒成立,求实数m的取值范围。
对一切实数x恒成立,求实数m的取值范围。