��Ŀ����
�������У�1����2����3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ʒ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������У�
��1����֪����M=
��N=
����MN=
��
������ʵ��a��b��c��d��ֵ��������ֱ��y=3x�ھ���M����Ӧ�����Ա任�µ���ķ��̣�
��2����ֱ������ϵxoy�У�ֱ��l�IJ�������Ϊ
��tΪ���������ڼ�����ϵ����ֱ������ϵxoyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ��=2
sin����
������ԲC��ֱ�����귽�̣�������ԲC��ֱ��l���ڵ�A��B������P������Ϊ(3��
)��
��|PA|+|PB|��
��3����֪����f��x��=|x-a|��
����������ʽf��x����3�Ľ⼯Ϊ{x|-1��x��5}����ʵ��a��ֵ��
�����ڣ��������£���f��x��+f��x+5����m��һ��ʵ��x���������ʵ��m��ȡֵ��Χ��
��1����֪����M=
|
|
|
������ʵ��a��b��c��d��ֵ��������ֱ��y=3x�ھ���M����Ӧ�����Ա任�µ���ķ��̣�
��2����ֱ������ϵxoy�У�ֱ��l�IJ�������Ϊ
|
| 5 |
������ԲC��ֱ�����귽�̣�������ԲC��ֱ��l���ڵ�A��B������P������Ϊ(3��
| 5 |
��|PA|+|PB|��
��3����֪����f��x��=|x-a|��
����������ʽf��x����3�Ľ⼯Ϊ{x|-1��x��5}����ʵ��a��ֵ��
�����ڣ��������£���f��x��+f��x+5����m��һ��ʵ��x���������ʵ��m��ȡֵ��Χ��
��1��ѡ��1�������������
�����
��
������Ϊ����M����Ӧ�����Ա任��ֱ�߱��ֱ�ߣ���㣩�����Կ�ȡֱ��y=3x�ϵ�����0��0������1��3����
��
=
��
=
��
�õ㣨0��0������1��3���ھ���M����Ӧ�ı任�µ��ߵ����ǣ�0��0������-2��2����
�Ӷ�ֱ��y=3x�ھ���M����Ӧ�����Ա任�µ���ķ���Ϊy=-x��
��2��ѡ��2�������ɦ�=2
sin�ȵ�x2+y2-2
y=0����x2+(y-
)2=5��
����l�IJ������̴���ԲC��ֱ�����귽�̣���(3-
t)2+(
t)2=5��
��t2-3
t+4=0��
������=(3
)2-4��4=2��0��
�ʿ���t1��t2���������̵���ʵ����
����
��
��ֱ��l����P��3��
����
������ʽ��t�ļ�������ã�
|PA|+|PB|=|t1|+|t2|=t1+t2=3
��
��3��ѡ��3��������f��x����3��|x-a|��3�����a-3��x��a+3��
����֪����ʽf��x����3�Ľ⼯Ϊ{x|-1��x��5}��
����
�����a=2��
����a=2ʱ��f��x��=|x-2|��
��g��x��=f��x��+f��x+5����
����g��x��=|x-2|+|x+3|=
��
���ԣ���x��-3ʱ��g��x����5��
��-3��x��2ʱ��g��x����5��
��x��2ʱ��g��x����5��
|
|
������Ϊ����M����Ӧ�����Ա任��ֱ�߱��ֱ�ߣ���㣩�����Կ�ȡֱ��y=3x�ϵ�����0��0������1��3����
��
|
|
|
|
|
|
�õ㣨0��0������1��3���ھ���M����Ӧ�ı任�µ��ߵ����ǣ�0��0������-2��2����
�Ӷ�ֱ��y=3x�ھ���M����Ӧ�����Ա任�µ���ķ���Ϊy=-x��
��2��ѡ��2�������ɦ�=2
| 5 |
| 5 |
| 5 |
����l�IJ������̴���ԲC��ֱ�����귽�̣���(3-
| ||
| 2 |
| ||
| 2 |
��t2-3
| 2 |
������=(3
| 2 |
�ʿ���t1��t2���������̵���ʵ����
����
|
��ֱ��l����P��3��
| 5 |
������ʽ��t�ļ�������ã�
|PA|+|PB|=|t1|+|t2|=t1+t2=3
| 2 |
��3��ѡ��3��������f��x����3��|x-a|��3�����a-3��x��a+3��
����֪����ʽf��x����3�Ľ⼯Ϊ{x|-1��x��5}��
����
|
����a=2ʱ��f��x��=|x-2|��
��g��x��=f��x��+f��x+5����
����g��x��=|x-2|+|x+3|=
|
���ԣ���x��-3ʱ��g��x����5��
��-3��x��2ʱ��g��x����5��
��x��2ʱ��g��x����5��

��ϰ��ϵ�д�
�����Ŀ
 ��N=
��N= ����MN=
����MN= ��
�� =2
=2 sin
sin ��
�� 3�Ľ⼯Ϊ
3�Ľ⼯Ϊ ����ʵ��a��ֵ��
����ʵ��a��ֵ��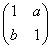 ��
��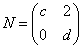 ����
����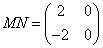 ��
��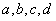 ��ֵ��������ֱ��
��ֵ��������ֱ��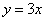 �ھ���M����Ӧ�����Ա任�µ���ķ��̡�
�ھ���M����Ӧ�����Ա任�µ���ķ��̡�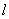 �IJ�������Ϊ
�IJ�������Ϊ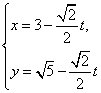 ��tΪ���������ڼ�����ϵ����ֱ������ϵxoyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ
��tΪ���������ڼ�����ϵ����ֱ������ϵxoyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ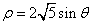 ��
��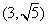 ��
��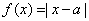 ��
��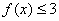 �Ľ⼯Ϊ
�Ľ⼯Ϊ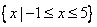 ����ʵ��
����ʵ��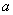 ��ֵ��
��ֵ��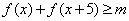 ��һ��ʵ��x���������ʵ��m��ȡֵ��Χ��
��һ��ʵ��x���������ʵ��m��ȡֵ��Χ�� ��
�� ����
���� ��
�� ��tΪ���������ڼ�����ϵ����ֱ������ϵxoyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ
��tΪ���������ڼ�����ϵ����ֱ������ϵxoyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ ��
�� ��
��