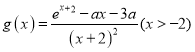题目内容
【题目】过直线
上一动点
不在
轴上)作焦点为
的抛物线
的两条切线, 
为切点,直线
分别与
轴交于点
.
(Ⅰ)求证: 
，并求
的外接圆面积的最小值；
(Ⅱ)求证:直线
恒过一定点。
【答案】(Ⅰ)证明见解析，外接圆面积最小值为： 
.(Ⅱ)证明见解析.
【解析】试题分析：(1)写出抛物线方程，联立直线和抛物线的方程，得到关于
的一元二次方程，利用判别式为0判定两直线垂直，进而求得外接圆的最小值；(2)先得到直线方程，再代点确定点的关系，进而得到直线
的方程，再验证恒过定点 .
试题解析：( I ) 
设
，则直线
为
，与
联立，得： 
因为相切，所以
，得： 
，又
，所以
即
，同理： 
，所以
为
的外接圆，又因为： 
，所以
的外接圆面积最小值为： 
.
（Ⅱ）设点
，
易知：直线
方程为： 
，
代入点
坐标得： 
，同理： 
，
所以直线
方程为： 
，又点
满足： 
所以直线
恒过定点
高中必刷题系列答案【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
转速x（转/秒） | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y（件） | 5 | 7 | 8 | 9 | 11 |
（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？
【题目】从一批土鸡蛋中，随机抽取n个得到一个样本，其重量（单位：克）的频数分布表如表：
分组（重量） | [80，85） | [85，90） | [90，95） | [95，100] |
频数（个） | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个，抽到重量在在[90，95）的土鸡蛋的根底为 
（1）求出n，m的值及该样本的众数；
（2）用分层抽样的方法从重量在[80，85）和[95，100）的土鸡蛋中共抽取5个，再从这5个土鸡蛋中任取2 个，其重量分别是g1 ， g2 ， 求|g1﹣g2|≥10概率．
