题目内容
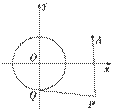
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
(Ⅰ)求椭圆C的标准方程;
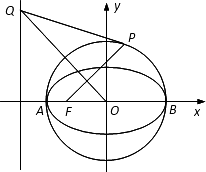
(Ⅱ)若点P的坐标为(1,1),求证:直线PQ与圆O相切;
(Ⅲ)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
答案:
解析:
解析:
|
(Ⅱ)因为P(1,1),所以 又椭圆的左准线方程为x=-2,所以点Q(-2,4) 所以kPQ=-1,又kQP=1,所以kOP⊥kQP=-1,即OP⊥PQ, 故直线PQ与圆O相切 (Ⅲ)当点P在圆O上运动时,直线PQ与圆O保持相切 证明:设P(x0,y0)( 所以直线OQ的方程为 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
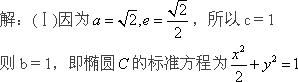

 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.