Question

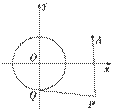
已知圆O：x²＋y²＝1和定点A(2,1)，由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，|PQ|＝|PA|成立，如图．

(1)求a、b间关系；

(2)求|PQ|的最小值；

(3)以P为圆心作圆，使它与圆O有公共点，试在其中求出半径最小的圆的方程．

Answer 1

解：(1)连接OQ、OP，则△OQP为直角三角形，

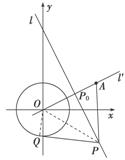
又|PQ|＝|PA|，

所以|OP|²＝|OQ|²＋|PQ|²

＝1＋|PA|²，

所以a²＋b²＝1＋(a－2)²＋(b－1)²，

故2a＋b－3＝0.

(2)由(1)知，P在直线l：2x＋y－3＝0上，

所以|PQ|_min＝|PA|_min，为A到直线l的距离，

所以|PQ|_min＝＝.

(或由|PQ|²＝|OP|²－1＝a²＋b²－1＝a²＋9－12a＋4a²－1＝5a²－12a＋8＝5(a－1.2)²＋0.8，得|PQ|_min＝.)

(3)以P为圆心的圆与圆O有公共点，半径最小时为与圆O相切的情形，而这些半径的最小值为圆O到直线l的距离减去圆O的半径，圆心P为过原点与l垂直的直线l′与l的交点P₀，所以r＝－1＝－1，

又l′：x－2y＝0，

联立l：2x＋y－3＝0得P₀(，)．

所以所求圆的方程为(x－)²＋(y－)²＝(－1)².