题目内容
已知数列{xn}的前n项和为Sn满足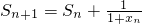 ,
,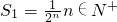
(I)猜想数列{x2n}的单调性,并证明你的结论;
(Ⅱ)对于数列{un}若存在常数M>0,对任意的n∈N+,恒有|un+1-un|+|un-un-1|+-+|u2-u1|≤M则称数列{Un}为B-数列.问数列{xn}是B-数列吗?并证明你的结论.
解:(I)由已知得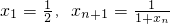 ,∴
,∴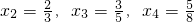 ,猜想数列{x2n}是递减数列(3分)
,猜想数列{x2n}是递减数列(3分)
下面用数学归纳法证明:
(1)当n=1时,已证命题成立(2)假设当n=k时命题成立,即x2k>x2k+2
易知x2k>0,那么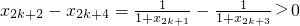 即x2(k+1)>x2(k+1)+2
即x2(k+1)>x2(k+1)+2
也就是说,当n=k+1时命题也成立,结合(1)和(2)知,命题成立(6分)
(Ⅱ)数列{xn}是B-数列.(7分)
当n=1时,|xn+1-xn|=|x2-x1|= ,(8分)
,(8分)
当n≥2时,易知0<xn-1<1,∴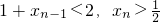 (9分)
(9分)
∴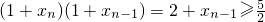 (10分)
(10分)
∴|xn+1-xn|=|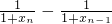 |=|xn-xn-1|×
|=|xn-xn-1|×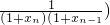
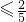 |xn-xn-1|≤-≤
|xn-xn-1|≤-≤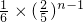 (12分)
(12分)
∴|xn+1-xn|+|xn-xn-1|+-+|x2-x1|≤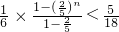
所以数列{xn}是B-数列.(13分)
分析:(I)由已知得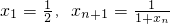 ,∴
,∴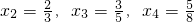 ,猜想数列{x2n}是递减数列,再用数学归纳法证明;
,猜想数列{x2n}是递减数列,再用数学归纳法证明;
(Ⅱ)利用定义寻找使得不等式成立的M的值,从而先去证明|xn+1-xn|≤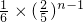 ,从而可判断.
,从而可判断.
点评:本题(1)中的证明要用到数学归纳法,数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.
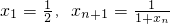 ,∴
,∴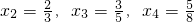 ,猜想数列{x2n}是递减数列(3分)
,猜想数列{x2n}是递减数列(3分)下面用数学归纳法证明:
(1)当n=1时,已证命题成立(2)假设当n=k时命题成立,即x2k>x2k+2
易知x2k>0,那么
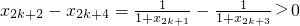 即x2(k+1)>x2(k+1)+2
即x2(k+1)>x2(k+1)+2也就是说,当n=k+1时命题也成立,结合(1)和(2)知,命题成立(6分)
(Ⅱ)数列{xn}是B-数列.(7分)
当n=1时,|xn+1-xn|=|x2-x1|=
 ,(8分)
,(8分)当n≥2时,易知0<xn-1<1,∴
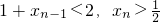 (9分)
(9分)∴
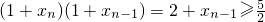 (10分)
(10分)∴|xn+1-xn|=|
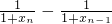 |=|xn-xn-1|×
|=|xn-xn-1|×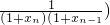
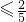 |xn-xn-1|≤-≤
|xn-xn-1|≤-≤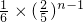 (12分)
(12分)∴|xn+1-xn|+|xn-xn-1|+-+|x2-x1|≤
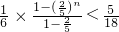
所以数列{xn}是B-数列.(13分)
分析:(I)由已知得
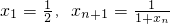 ,∴
,∴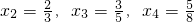 ,猜想数列{x2n}是递减数列,再用数学归纳法证明;
,猜想数列{x2n}是递减数列,再用数学归纳法证明;(Ⅱ)利用定义寻找使得不等式成立的M的值,从而先去证明|xn+1-xn|≤
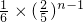 ,从而可判断.
,从而可判断.点评:本题(1)中的证明要用到数学归纳法,数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.

练习册系列答案
相关题目
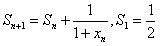 ,n∈N*。
,n∈N*。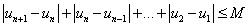 ,则称数列{un}为B-数列。问数列{xn}是B-数列吗? 并证明你的结论。
,则称数列{un}为B-数列。问数列{xn}是B-数列吗? 并证明你的结论。