题目内容
定义在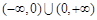 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在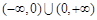 上的如下函数:
上的如下函数:
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
则其中是“保等比数列函数”的 的序号为( )
的序号为( )
A.① ② B.③ ④ C.① ③ D.② ④
【答案】
C
【解析】本题考查等比数列性质及函数计算,正确运算,理解新定义是解题的关键
因为由等比数列性质知anan+2=an+12,①f(an)f(an+2)=an2an+22=(an+12) 2=f2(an+1),故正确;
②根据解析式可知f(an)f(an+2)=2an2an+2= 2an+an+2≠22an+1=f2(an+1),故不正确;
③结合已知条件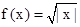 ,则f(an)f(an+2)=
,则f(an)f(an+2)=  f2(an+1),故正确;
f2(an+1),故正确;
④因为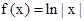 ,那么f(an)f(an+2)=ln|an|ln|an+2|≠ln|an+1|2=f2(an+1),故不正确;
,那么f(an)f(an+2)=ln|an|ln|an+2|≠ln|an+1|2=f2(an+1),故不正确;
故选C。
解决该试题的关键是根据新定义,结合等比数列性质anan+2=an+12,一一加以判断,即可得到结论。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 上的函数
上的函数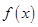 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称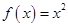 ②
② ③
③ ④
④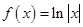
 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,  仍是等比数列,则称
仍是等比数列,则称 ; ②
; ② ; ③
; ③ ; ④
; ④ .则其中是“保等比数列函数”的
.则其中是“保等比数列函数”的 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 仍是等比数列,则称
仍是等比数列,则称 ;②
;② ;③
;③ ;④
;④ 。则其中是“保等比数列函数”的
。则其中是“保等比数列函数”的 上的函数
上的函数 ,如果
,如果 ,则实数
,则实数 的取值范围为______
的取值范围为______