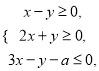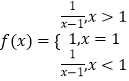Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥–£łŖ∂Ģįňįŗ—°≥Ųľ◊°Ę““°ĘĪŻ»ż√ŻÕ¨—ß≤őľ”ľ∂≤Ņ◊ť÷ĮĶńŅ∆—ß÷™ ∂ĺļ»Ł£ģ‘ŕł√īőĺļ»Ł÷–÷Ľ…Ť≥…ľ®”Ň–„ļÕ≥…ľ®Ńľļ√ŃĹłŲĶ»īő£¨»Űń≥Õ¨—ß≥…ľ®”Ň–„£¨‘ڳݔŤįŗľ∂10∑÷Ķńįŗľ∂Ľż∑÷£¨»Ű≥…ľ®Ńľļ√£¨‘ڳݔŤįŗľ∂5∑÷Ķńįŗľ∂Ľż∑÷£ģľŔ…Ťľ◊°Ę““°ĘĪŻ≥…ľ®ő™”Ň–„ĶńłŇ¬ ∑÷Īūő™ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨ňŻ√«Ķńĺļ»Ł≥…ľ®ŌŗĽ•∂ņŃĘ£ģ
£¨ňŻ√«Ķńĺļ»Ł≥…ľ®ŌŗĽ•∂ņŃĘ£ģ
£®1£©«ů‘ŕł√īőĺļ»Ł÷–ľ◊°Ę““°ĘĪŻ»ż√ŻÕ¨—ß÷–÷Ń…Ŕ”–“Ľ√Ż≥…ľ®ő™”Ň–„ĶńłŇ¬ £Ľ
£®2£©ľ«‘ŕł√īőĺļ»Ł÷–ľ◊°Ę““°ĘĪŻ»ż√ŻÕ¨—ßňýĶ√Ķńįŗľ∂Ľż∑÷÷ģļÕő™ňśĽķĪšŃŅ¶ő£¨«ůňśĽķĪšŃŅ¶őĶń∑÷≤ľŃ–ļÕ ż—ß∆ŕÕŻE¶ő£ģ
°ĺīūįł°Ņ
£®1£©Ĺ‚£ļľ«°įľ◊≥…ľ®ő™”Ň–„°Īő™ ¬ľĢA£¨°į““≥…ľ®”Ň–„°Īő™ ¬ľĢB£¨°įĪŻ≥…ľ®”Ň–„°Īő™ ¬ľĢC£¨
°įľ◊°Ę““°ĘĪŻ÷Ń…Ŕ”–“Ľ√Ż≥…ľ®ő™”Ň–„°Īő™ ¬ľĢE£¨
°Ŗ ¬ľĢA°ĘB°ĘC «ŌŗĽ•∂ņŃĘ ¬ľĢ£¨ ¬ľĢABC”Ž ¬ľĢE «∂‘ŃĘ ¬ľĢ£¨
°ŗP£®E£©=1©ĀP£® ![]() £©=1©Ā
£©=1©Ā ![]() =
= ![]()
£®2£©Ĺ‚£ļ¶őĶńňý”–Ņ…ń‹»°÷Ķő™15£¨20£¨25£¨30£¨
P£®¶ő=15£©=P£® ![]() £©=
£©= ![]() =
= ![]() £¨
£¨
P£®¶ő=20£©=P£®A ![]() £©+P£®
£©+P£® ![]() £©+P£®
£©+P£® ![]() £©=
£©= ![]() +
+ ![]() +
+ ![]() =
= ![]() £¨
£¨
P£®¶ő=30£©=P£®ABC£©= ![]() =
= ![]() £¨
£¨
°ŗ¶őĶń∑÷≤ľŃ–ő™£ļ
¶ő | 15 | 20 | 25 | 30 |
P |
|
|
|
|
E¶ő= ![]() =
= ![]()
°ĺĹ‚őŲ°Ņ£®1£©ľ«°įľ◊≥…ľ®ő™”Ň–„°Īő™ ¬ľĢA£¨°į““≥…ľ®”Ň–„°Īő™ ¬ľĢB£¨°įĪŻ≥…ľ®”Ň–„°Īő™ ¬ľĢC£¨°įľ◊°Ę““°ĘĪŻ÷Ń…Ŕ”–“Ľ√Ż≥…ľ®ő™”Ň–„°Īő™ ¬ľĢE£¨”… ¬ľĢA°ĘB°ĘC «ŌŗĽ•∂ņŃĘ ¬ľĢ£¨ ¬ľĢABC”Ž ¬ľĢE «∂‘ŃĘ ¬ľĢ£¨ń‹«ů≥Ų‘ŕł√īőĺļ»Ł÷–ľ◊°Ę““°ĘĪŻ»ż√ŻÕ¨—ß÷–÷Ń…Ŕ”–“Ľ√Ż≥…ľ®ő™”Ň–„ĶńłŇ¬ £ģ£®2£©¶őĶńňý”–Ņ…ń‹»°÷Ķő™15£¨20£¨25£¨30£¨∑÷Īū«ů≥ŲŌŗ”¶ĶńłŇ¬ £¨”…īňń‹«ů≥Ų¶őĶń∑÷≤ľŃ–ļÕE¶ő£ģ
°ĺŅľĶ„ĺęőŲ°ŅĹ‚īūīňŐ‚ĶńĻōľŁ‘ŕ”ŕņŪĹ‚ņŽ…Ę–ÕňśĽķĪšŃŅľį∆š∑÷≤ľŃ–ĶńŌŗĻō÷™ ∂£¨’∆ő’‘ŕ…šĽų°Ę≤ķ∆∑ľž—ťņż◊”÷–£¨∂‘”ŕňśĽķĪšŃŅXŅ…ń‹»°Ķń÷Ķ£¨ő“√«Ņ…“‘įī“Ľ∂®īő–Ú“Ľ“ĽŃ–≥Ų£¨’‚—ýĶńňśĽķĪšŃŅĹ–◊ŲņŽ…Ę–ÕňśĽķĪšŃŅ£ģņŽ…Ę–ÕňśĽķĪšŃŅĶń∑÷≤ľŃ–£ļ“Ľį„Ķń,…ŤņŽ…Ę–ÕňśĽķĪšŃŅXŅ…ń‹»°Ķń÷Ķő™x1,x2,.....,xi,......,xn£¨X»°√Ņ“ĽłŲ÷Ķ xi(i=1,2,......£©ĶńłŇ¬ P(¶ő=xi£©£ĹPi£¨‘Ú≥∆ĪŪő™ņŽ…Ę–ÕňśĽķĪšŃŅX ĶńłŇ¬ ∑÷≤ľ£¨ľÚ≥∆∑÷≤ľŃ–£ģ

 53ňśŐ√≤‚ŌĶŃ–īūįł
53ňśŐ√≤‚ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ ģįňĹžőŚ÷–»ęĽŠĻęĪ®÷ł≥Ų£ļҨѶīŔĹÝ»ňŅŕĺýļ‚∑Ę’Ļ£¨ľŠ≥÷ľ∆Ľģ…ķ”żĶńĽýĪĺĻķ≤Ŗ£¨ÕÍ…∆»ňŅŕ∑Ę’Ļ’Ŭ‘£¨»ę√ś Ķ ©“Ľ∂‘∑ÚłĺŅ……ķ”żŃĹłŲļĘ◊”Ķń’Ģ≤Ŗ£¨ŐŠłŖ…ķ÷≥Ĺ°ŅĶ°Ęłĺ”◊Ī£Ĺ°°ĘÕ–”◊Ķ»ĻęĻ≤∑ĢőŮňģ∆Ĺ£ģő™ŃňĹ‚ ŃšĻęőŮ‘Ī∂‘∑ŇŅ™…ķ”ż∂ĢŐ•’Ģ≤ŖĶńŐ¨∂»£¨ń≥≤Ņ√ŇňśĽķĶų≤ťŃň100őĽ30ĶĹ40ňÍĶńĻęőŮ‘Ī£¨Ķ√ĶĹ«ťŅŲ»ÁŌ¬ĪŪ£ļ
ń–ĻęőŮ‘Ī | ŇģĻęőŮ‘Ī | |
…ķ∂ĢŐ• | 40 | 20 |
≤Ľ…ķ∂ĢŐ• | 20 | 20 |
£®1£© «∑Ů”–95%“‘…ŌĶńį—ő’»Ōő™°į…ķ∂ĢŐ•”Ž–‘Īū”–Ļō°Ī£¨≤ĘňĶ√ųņŪ”…£Ľ
£®2£©į—“‘…Ō∆Ķ¬ ĶĪłŇ¬ £¨»Űī”…ÁĽŠ…ŌňśĽķ≥ť»°3őĽ30ĶĹ40ňÍĶńń–ĻęőŮ‘Ī£¨ľ«∆š÷–…ķ∂ĢŐ•Ķń»ň żő™X£¨«ůňśĽķĪšŃŅXĶń∑÷≤ľŃ–£¨ ż—ß∆ŕÕŻ£ģ
łĹ£ļK2= ![]()
P£®K2°›k0£© | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |