题目内容
 如图,在四面体PABC中,点D,E,F,分别是棱AP,AC,BC的中点.
如图,在四面体PABC中,点D,E,F,分别是棱AP,AC,BC的中点.(1)若G为PB的中点,且PC⊥AB,求证:四边形DEFG为矩形;
(2)过D,E,F的平面与PB交于G,试确定四边形DEFG的形状?并说明理由?
分析:(1)运用三角形的中位线平行于底边及平行公理得到四边形DEFG为平行四边形,再根据PC⊥AB得到四边形的一个内角为直角;
(2)由线面平行的判定得到PC和AB都与平面DEF平行,再由线面平行的性质定理及平行公理得到四边形的两组对边平行.
(2)由线面平行的判定得到PC和AB都与平面DEF平行,再由线面平行的性质定理及平行公理得到四边形的两组对边平行.
解答:(1)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE∥PC∥FG,DG∥AB∥EF,
所以四边形DEFG为平行四边形.
又因为PC⊥AB,所以DE⊥DG,所以四边形DEFG为矩形.

(2)四边形DEFG为平行四边形.
证明:因为D,E分别为AP,AC的中点,所以DE∥PC
∵DE?平面BPC,PC?平面BPC,∴DE∥平面BPC
∵DE?平面DEFG,且平面APC∩平面BPC=FG,
∴DE∥FG,同理EF∥DG,
所以四边形为平行四边形.
所以DE∥PC∥FG,DG∥AB∥EF,
所以四边形DEFG为平行四边形.
又因为PC⊥AB,所以DE⊥DG,所以四边形DEFG为矩形.

(2)四边形DEFG为平行四边形.
证明:因为D,E分别为AP,AC的中点,所以DE∥PC
∵DE?平面BPC,PC?平面BPC,∴DE∥平面BPC
∵DE?平面DEFG,且平面APC∩平面BPC=FG,
∴DE∥FG,同理EF∥DG,
所以四边形为平行四边形.
点评:本题考查了棱锥的结构特征,考查了线面平行的判定定理和性质定理,考查了学生的逻辑思维能力,此题是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
(2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.

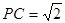 ,求四面体PABC的体积.
,求四面体PABC的体积. 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.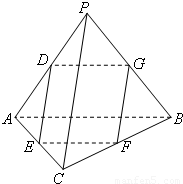 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.