题目内容
斜率为1的直线l与椭圆 +y2=1相交于A、B两点,则|AB|的最大值为( )
+y2=1相交于A、B两点,则|AB|的最大值为( )A.2
B.

C.

D.

【答案】分析:设出直线的方程,代入椭圆方程中消去y,根据判别式大于0求得t的范围,进而利用弦长公式求得|AB|的表达式,利用t的范围求得|AB|的最大值.
解答:解:设直线l的方程为y=x+t,代入 +y2=1,消去y得
+y2=1,消去y得 x2+2tx+t2-1=0,
x2+2tx+t2-1=0,
由题意得△=(2t)2-5(t2-1)>0,即t2<5.
弦长|AB|=4 ×
× ≤
≤ .
.
故选C
点评:本题主要考查了椭圆的应用,直线与椭圆的关系.常需要把直线与椭圆方程联立,利用韦达定理,判别式找到解决问题的突破口.
解答:解:设直线l的方程为y=x+t,代入
 +y2=1,消去y得
+y2=1,消去y得 x2+2tx+t2-1=0,
x2+2tx+t2-1=0,由题意得△=(2t)2-5(t2-1)>0,即t2<5.
弦长|AB|=4
 ×
× ≤
≤ .
.故选C
点评:本题主要考查了椭圆的应用,直线与椭圆的关系.常需要把直线与椭圆方程联立,利用韦达定理,判别式找到解决问题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点.
,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点. ,直线l过点M(b,0),且
,直线l过点M(b,0),且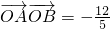 ,求椭圆C的方程;
,求椭圆C的方程; =λ(
=λ( +
+ )(λ>0),若点P在椭C上,λ的取值范围.
)(λ>0),若点P在椭C上,λ的取值范围.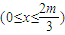 和椭圆弧
和椭圆弧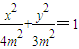

 和椭圆弧
和椭圆弧
