题目内容
椭圆C的方程 ,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点.
,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点.
(Ⅰ)若椭圆的离心率 ,直线l过点M(b,0),且
,直线l过点M(b,0),且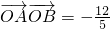 ,求椭圆C的方程;
,求椭圆C的方程;
(Ⅱ)直线l过椭圆的右焦点F,设向量 =λ(
=λ( +
+ )(λ>0),若点P在椭C上,λ的取值范围.
)(λ>0),若点P在椭C上,λ的取值范围.
解:(Ⅰ)∵ ,∴a=2b,c=
,∴a=2b,c=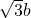 .
.
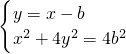 ,
,
∴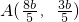 ,B(0,-b).
,B(0,-b).
∵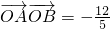 ,∴-
,∴-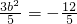 ,b2=4,a2=16.
,b2=4,a2=16.
∴椭圆C的方程为 .(5分)
.(5分)
(Ⅱ)由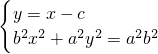 ,
,
得(b2+a2)x2-2a2cx+a2(c2-b2)=0,
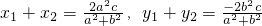 .
.
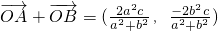 ,
,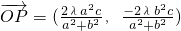 .
.
∵点P在椭圆C上,将点P坐标代入椭圆方程中得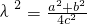 .
.
∵b2+c2=a2,0<e<1,
∴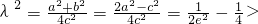
 ,
,
∴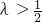 .(12分)
.(12分)
分析:(Ⅰ)由 ,知a=2b,c=
,知a=2b,c=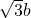 .由
.由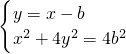 ,知
,知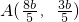 ,B(0,-b).再由
,B(0,-b).再由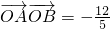 能推导出椭圆C的方程.
能推导出椭圆C的方程.
(Ⅱ)由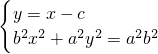 ,得(b2+a2)x2-2a2cx+a2(c2-b2)=0,由韦达定理知
,得(b2+a2)x2-2a2cx+a2(c2-b2)=0,由韦达定理知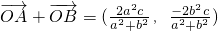 ,
,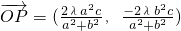 .再由点P在椭圆C上,知
.再由点P在椭圆C上,知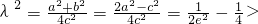
 ,由此能导出λ的取值范围.
,由此能导出λ的取值范围.
点评:本题考查椭圆方程的求法和求实数λ的取值范围.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 ,∴a=2b,c=
,∴a=2b,c=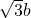 .
.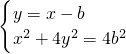 ,
,∴
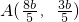 ,B(0,-b).
,B(0,-b).∵
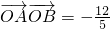 ,∴-
,∴-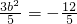 ,b2=4,a2=16.
,b2=4,a2=16.∴椭圆C的方程为
 .(5分)
.(5分)(Ⅱ)由
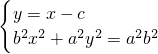 ,
,得(b2+a2)x2-2a2cx+a2(c2-b2)=0,
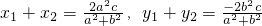 .
.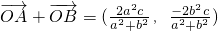 ,
,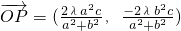 .
.∵点P在椭圆C上,将点P坐标代入椭圆方程中得
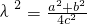 .
.∵b2+c2=a2,0<e<1,
∴
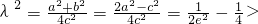
 ,
,∴
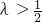 .(12分)
.(12分)分析:(Ⅰ)由
 ,知a=2b,c=
,知a=2b,c=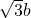 .由
.由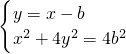 ,知
,知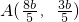 ,B(0,-b).再由
,B(0,-b).再由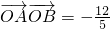 能推导出椭圆C的方程.
能推导出椭圆C的方程.(Ⅱ)由
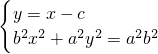 ,得(b2+a2)x2-2a2cx+a2(c2-b2)=0,由韦达定理知
,得(b2+a2)x2-2a2cx+a2(c2-b2)=0,由韦达定理知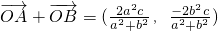 ,
,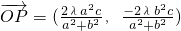 .再由点P在椭圆C上,知
.再由点P在椭圆C上,知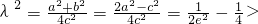
 ,由此能导出λ的取值范围.
,由此能导出λ的取值范围.点评:本题考查椭圆方程的求法和求实数λ的取值范围.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
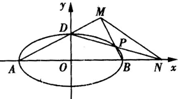 (2013•江西)椭圆C:
(2013•江西)椭圆C: 如图所示,椭圆C:
如图所示,椭圆C: