题目内容
研究一下,是否存在一个三角形具有以下性质:
(1)
三边是连续的三个自然数;(2)
最大角是最小角的2倍.
答案:略
解析:
解析:
|
设三角形三边长分别是 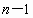 ,n, ,n,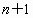 ,三个角分别是 ,三个角分别是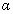 , ,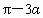 , ,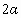 .由正弦定理, .由正弦定理,
所以,
由余弦定理,
即
化简,得
所以, n=0,或n=5.n=0不合题意,舍去.n=5.三角形的三边分别是4,5,6.可以验证此三角形的最大角是最小角的2倍.另解:先考虑三角形所具有的第一个性质:三边是连续的三个自然数. (1)三边的长不可能是1,2,3.这是因为1+2=3,而三角形任何两边之和大于第三边. (2)如果三边分别是a=2,b=3,c=4. 因为
在此三角形中, A是最小角,C是最大角,但是,
所以,
边长为 2,3,4的三角形不满足条件.(3)如果三边分别是a=3,b=4,c=5,此三角形是直角三角形,最大角是90°,最小角不等于45°,此三角形不满足条件. (4)如果三边是a=4,b=5,c=6.此时,
因为
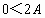 , ,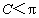 , ,
所以,
所以,边长为 4,5,6的三角形满足条件.(5)当 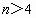 ,三角形的三边是a=n,b=n+1,c=n+2时,三角形的最小角是A,最大角是C. ,三角形的三边是a=n,b=n+1,c=n+2时,三角形的最小角是A,最大角是C.
cosA 随n的增大而减小,A随之增大,cosC随n的增大而增大,C随之变小.由于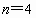 时有C=2A,所以, 时有C=2A,所以,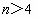 时,不可能 时,不可能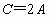 . .
综上可知,只有边长分别为 4,5,6的三角形满足条件. |

练习册系列答案
相关题目
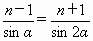
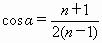
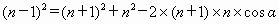
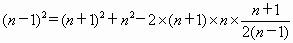
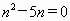
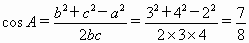
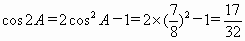
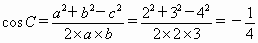
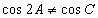
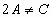
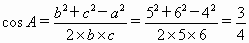
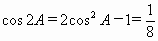
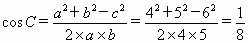
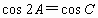

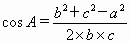
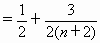
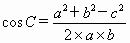
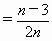
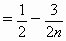
 如图,椭圆
如图,椭圆