题目内容
15．若f（sinx）=1-2sin2x，则$f（{\frac{{\sqrt{3}}}{2}}）$的值是$-\frac{1}{2}$．分析 直接利用条件可得f（x）=1-2x2，从而求得$f（{\frac{{\sqrt{3}}}{2}}）$的值．
解答 解：∵f（sinx）=1-2sin2x，
∴f（x）=1-2x2，则$f（{\frac{{\sqrt{3}}}{2}}）$=1-2×${（\frac{\sqrt{3}}{2}）}^{2}$=-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．
点评 本题主要考查求函数的值，属于基础题．
练习册系列答案
相关题目
6．已知幂函数y=f（x）的图象过点$（2，\sqrt{2}）$，则f（9）=（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | 9 | D． | $\frac{1}{9}$ |
3．已知f（x）=x2+ax在[0，1]上是单调递减函数，则实数a的取值范围是（ ）
| A． | （-∞，2] | B． | （-∞，-2] | C． | [0，+∞） | D． | [2，+∞） |
10．已知$\overrightarrow a$=（3，0），$\overrightarrow b$=（-5，5）则$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{2π}{3}$ |
20．20152015除以8的余数为（ ）
| A． | 1 | B． | 3 | C． | 5 | D． | 7 |
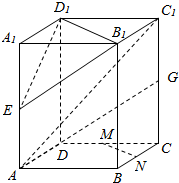如图所示，在平行六面体ABCD-A1B1C1D1中，E．M．N．G分别是AA1，CD，CB，CC1的中点，求证：
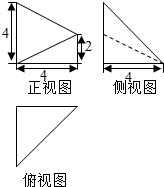已知几何体A-BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，已知几何体A-BCED的体积为16．将直角三角形△ABD绕斜边AD旋转一周，则BD=2；该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$．