题目内容
【题目】奇函数f（x）、偶函数g（x）的图象分别如图1、2所示，方程f（g（x））=0、g（f（x））=0的实根个数分别为a、b，则a+b=（ ） 
A.14
B.10
C.7
D.3
【答案】B
【解析】解：由图可知，图1为f（x）图象，图2为g（x）的图象，m∈（﹣2，﹣1），n∈（1，2）
∴方程f（g（x））=0g（x）=﹣1或g（x）=0或g（x）=1x=﹣1，x=1，x=m，x=0，x=n，x=﹣2，x=2，∴方程f（g（x））=0有7个根，即a=7；
而方程g（f（x））=0f（x）=a或f（x）=0或f（x）=bf（x）=0x=﹣1，x=0，x=1，∴方程g（f（x））=0 有3个根，即b=3
∴a+b=10
故选 B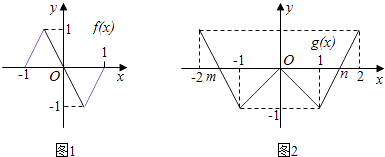
练习册系列答案
名校课堂系列答案
相关题目
