题目内容
已知x、y满足
记点(x,y)对应的平面区域为P.
(Ⅰ)设z=
,求z的取值范围;
(Ⅱ)过点(-5,1)的一束光线,射到x轴被反射后经过区域P,当反射光线所在直线l经过区域P内的整点(即横纵坐标均是整数的点)时,求直线l的方程.
|
(Ⅰ)设z=
| y+1 |
| x+3 |
(Ⅱ)过点(-5,1)的一束光线,射到x轴被反射后经过区域P,当反射光线所在直线l经过区域P内的整点(即横纵坐标均是整数的点)时,求直线l的方程.
分析:(1)作出可行域,z的几何意义为动动Q到定点P(-3,-1)的斜率.
(2)利用反射光线的性质确定直线的斜率,然后求出直线的方程.
(2)利用反射光线的性质确定直线的斜率,然后求出直线的方程.
解答: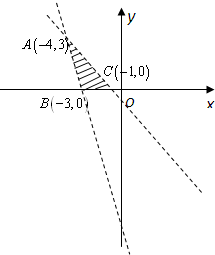 解:平面区域如图所示,易得A、B、C三点坐标分别为A(-4,3)、B(-3,0)、C(-1,0).
解:平面区域如图所示,易得A、B、C三点坐标分别为A(-4,3)、B(-3,0)、C(-1,0).
(Ⅰ)由z=
知z的值即是定点P(-1,-3)与区域内的点Q(x,y)连接的直线的斜率,
当直线过A(-4,3)时,z=-4;
当直线过C(-1,0)时,z=
.
故z的取值范围是(-∞,-4)∪(
,+∞).…(6分)
(Ⅱ)过点(-5,1)的光线被x轴反射后的光线所在直线必经过点(-5,-1),由
题设可得区域内坐标为整数点仅有点(-3,1),
故直线l的方程是
=
,即x-y+4=0.
…(12分)
 解:平面区域如图所示,易得A、B、C三点坐标分别为A(-4,3)、B(-3,0)、C(-1,0).
解:平面区域如图所示,易得A、B、C三点坐标分别为A(-4,3)、B(-3,0)、C(-1,0).(Ⅰ)由z=
| y+1 |
| x+3 |
当直线过A(-4,3)时,z=-4;
当直线过C(-1,0)时,z=
| 1 |
| 2 |
故z的取值范围是(-∞,-4)∪(
| 1 |
| 2 |
(Ⅱ)过点(-5,1)的光线被x轴反射后的光线所在直线必经过点(-5,-1),由
题设可得区域内坐标为整数点仅有点(-3,1),
故直线l的方程是
| y-1 |
| (-1)-1 |
| (x+3) |
| (-5)+3 |
…(12分)
点评:本题主要考查线性规划的简单应用,利用z的几何意义求最值是解决本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目