Question

已知x，y满足

y-2≤0 x+3≥0 x-y-1≤0

，则x²+y²最大值为

 

．

Answer 1

分析：先根据约束条件画出可行域，再利用几何意义求最值，z=x²+y²表示动点到原点的距离的平方，只需求出可行域内的动点到原点的距离最大值即可．

解答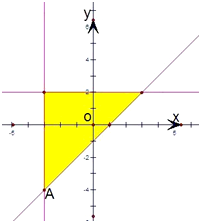：解：注意到目标函数所表示的几何意义是动点到原点的距离的平方，
作出可行域．如图．
易知当为A点时取得目标函数的最大值，
可知A点的坐标为（-3，-4），
代入目标函数中，可得z_max=3²+4²=25．
故答案为：25．

点评：本题属于线性规划中的延伸题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与原点之间的距离问题