题目内容
15. 用一边长为1米,另一边长为a米的矩形铁皮做一个无盖的长方形容器,先在四角分别截去一个的边长为x米的小正方形,然后把四边翻折90°角,再焊接而成.设该容器的容积为f(x).
用一边长为1米,另一边长为a米的矩形铁皮做一个无盖的长方形容器,先在四角分别截去一个的边长为x米的小正方形,然后把四边翻折90°角,再焊接而成.设该容器的容积为f(x).(1)求f(x)的表达式,并写出它的定义域;
(2)若0<a<1,试判断x取何值时,容器的容积达到最大或最小,并说明理由.
分析 (1)设容器的高为xcm,利用体积公式,可得f(x)的表达式,并写出它的定义域;
(2)设容器的高为xcm,得容器的容积为V(x)与x之间的关系,为三次函数,求导,利用函数的单调性求出函数的最值.
解答 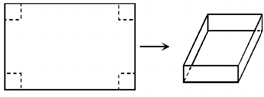 解:(1)设容器的高为xcm,容器的容积为V(x)cm3,则
解:(1)设容器的高为xcm,容器的容积为V(x)cm3,则
V(x)=(1-2x)(a-2x)x=4x3-(2a+2)x2+ax(0<x<$\frac{1}{2}$或0<x<$\frac{a}{2}$),
(2)V′(x)=12x2-(4a+4)x+a=0,可得x=$\frac{a+1±\sqrt{{a}^{2}-a+1}}{6}$,
∵0<a<1,0<x<$\frac{1}{2}$
∴当0<x<$\frac{a+1-\sqrt{{a}^{2}-a+1}}{6}$,$\frac{a+1+\sqrt{{a}^{2}-a+1}}{6}$<x<$\frac{1}{2}$时,V′(x)>0,当$\frac{a+1-\sqrt{{a}^{2}-a+1}}{6}$<x<$\frac{a+1+\sqrt{{a}^{2}-a+1}}{6}$时,V′(x)<0,
∴当x=$\frac{a+1-\sqrt{{a}^{2}-a+1}}{6}$时,V(x)在区间(0,1)内有唯一极大值,
∴容器高x=$\frac{a+1-\sqrt{{a}^{2}-a+1}}{6}$时,容器容积V(x)最大.
点评 本题考查导数在最大值问题中的应用,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1的渐近线上一点A到双曲线的右焦点F的距离等于2,抛物线y2=2px(p>0)过点A,则该抛物线的方程为( )
| A. | y2=9x | B. | y2=4x | C. | y2=$\frac{4\sqrt{13}}{13}$x | D. | y2=$\frac{2\sqrt{13}}{13}$x |