题目内容
10．求导：y=$\frac{sin2x}{2x-1}$．分析 根据导数的运算法则进行求导即可．
解答 解：函数的导数f′（x）=$\frac{2cos2x•（2x-1）-sin2x•2}{（2x-1）^{2}}$=$\frac{（4x-2）cos2x-2sin2x}{（2x-1）^{2}}$．
点评 本题主要考查导数的计算，要求熟练掌握掌握常见函数的导数公式以及导数的运算法则，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
1．已知直线ax+y+1=0经过抛物线y2=4x的焦点，则直线与抛物线相交弦弦长为（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
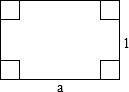用一边长为1米，另一边长为a米的矩形铁皮做一个无盖的长方形容器，先在四角分别截去一个的边长为x米的小正方形，然后把四边翻折90°角，再焊接而成．设该容器的容积为f（x）．
20．
如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P、Q，若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$，则双曲线C的离心率为（ ）
如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P、Q，若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$，则双曲线C的离心率为（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{7}}{2}$ | C． | $\frac{\sqrt{39}}{6}$ | D． | $\sqrt{3}$ |