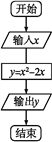
题目内容
【题目】已知全集U=R,集合A={x|x2-11x+18<0},B={x|-2≤x≤5}.
(1)求A∩B;B∪(UA);
(2)已知集合C={x|a≤x≤a+2},若C∩![]() =C,求实数a的取值范围.
=C,求实数a的取值范围.
【答案】(1){x|2<x≤5}; {x|x≤5或x≥9}(2)(-∞,-4)∪(5,+∞)
【解析】
(1)化简集合A,根据补集与并集和交集的定义计算即可;(2)根据题意,利用集合的定义与运算性质,列不等式组求出a的取值范围.
(1)集合A={x|x2-11x+18<0}={x|2<x<9},
全集U=R,则UA={x|x≤2或x≥9};
又B={x|-2≤x≤5},则A∩B={x|2<x≤5};
∴B∪(UA)={x|x≤5或x≥9};
(2)集合C={x|a≤x≤a+2},B={x|-2≤x≤5},
则:UB={x|x<-2或x>5},
∵C∩UB=C,
∴CUB,
∴需满足:a+2<-2或a>5,
解得:a<-4或a>5,
所以实数a的取值范围是(-∞,-4)∪(5,+∞).

练习册系列答案
相关题目
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在图中的两条线段上;该股票在30天内的日交易量
落在图中的两条线段上;该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如下表所示,且
(天)的部分数据如下表所示,且![]() 与
与![]() 满足一次函数关系,
满足一次函数关系,

第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
那么在这30天中第几天日交易额最大( )
A. 10 B. 15 C. 20 D. 25