题目内容
设函数f ( x ) = ![]() (a ??N*), 又存在非零自然数m, 使得f (m ) = m ,
(a ??N*), 又存在非零自然数m, 使得f (m ) = m ,
f (– m ) < –![]() 成立.
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若![]() 对任意n??N*成立, 求数列{an}的一个通项公式;
对任意n??N*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
(1)f ( x ) = ![]() ( x ?? 1).
( x ?? 1).
(2) an= – 1 + (n – 1 )( – 1)= – n .
(3)满足条件的数列不惟一.
解析:
(1) 由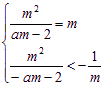 , 得
, 得![]()
由(1)得 m = ![]() ,
,
当a = 2时, m = 2, 满足(2)式;
当a = 3时, m = 1, 不满足(2)式, 舍去. 得f ( x ) = ![]() ( x ?? 1).
( x ?? 1).
(2) 由条件得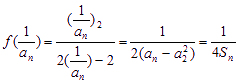
∴ an(1 – an) = 2Sn (3) ,
令n = 1,得 a1 = –1,
又an – 1 (1 – an – 1 ) = 2S n – 1 , ∴( an + a n – 1 )( an + 1 – a n – 1 )= 0,
由an – a n – 1 = – 1 , a1 = –1,得{an}是首项为– 1, 公差为– 1的等差数列,
∴ an= – 1 + (n – 1 )( – 1)= – n .
(3) 由(2)知,满足条件的数列不惟一.
考虑到a1 ?? 1, 由 an = – a n – 1 及an – a n – 1 = – 1和a1 = –1,
构造数列{ –1, –2, 2,–2, –3, – 4, … , – n +2, … }.
用数学归纳法证明,该数列满足(3)式,
当n = 1, 2, 3, 4, 5时,直接代入可得(3)式成立,
假设n = k ( k ?? 5)时,(3)成立, 则n = k + 1时,
Sk+1 =S k + a k+1 = ![]() ak(1 – ak) + a k + 1 =
ak(1 – ak) + a k + 1 = ![]() (–a k +1)(1 + ak+1) + a k + 1 =
(–a k +1)(1 + ak+1) + a k + 1 =![]() ak+1(1 – a k+1).
ak+1(1 – a k+1).
所以n = k + 1时(3)式成立, 即该数列满足题设条件.
得满足条件的数列不惟一.
构造数列也可能是:
{ –1, 1, –1, –2, –3, – 4, … , – n , … };
{ –1, –2,2, –2, 2, –2, … , (–1) n – 1 2 , … }( n > 1 )
{ –1, –2,2, –2, –3, – 4, … , – n , … }等等.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
(2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )