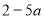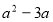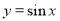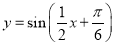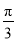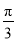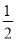题目内容
设函数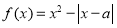 (
(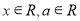 ).
).
(1)若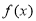 为偶函数,求实数
为偶函数,求实数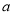 的值;
的值;
(2)已知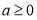 ,若对任意
,若对任意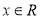 都有
都有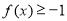 恒成立,求实数
恒成立,求实数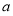 的取值范围.
的取值范围.
(1)0;(2)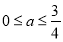
【解析】
试题分析:(1)根据偶函数定义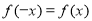 ,得到
,得到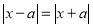 ,平方后可根据对应系数相等得到a的值,也可将上式两边平方得
,平方后可根据对应系数相等得到a的值,也可将上式两边平方得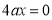 恒成立,得a的值。(2)应先去掉绝对值将其改写为分段函数,在每段上求函数
恒成立,得a的值。(2)应先去掉绝对值将其改写为分段函数,在每段上求函数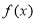 在
在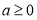 时的最小值,在每段求最值时都属于定轴动区间问题,需讨论。最后比较这两个最小值的大小取最小的那个,即为原函数的最小值。要使
时的最小值,在每段求最值时都属于定轴动区间问题,需讨论。最后比较这两个最小值的大小取最小的那个,即为原函数的最小值。要使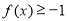 恒成立,只需
恒成立,只需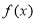 的最小值大于等于1即可,从而求得a的范围
的最小值大于等于1即可,从而求得a的范围
试题解析:(1)若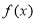 的为偶函数,则
的为偶函数,则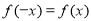
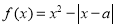 ,
,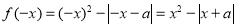 ,
,
故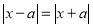 ,
,
两边平方得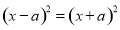 ,展开
,展开
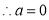 时,
时,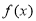 为偶函数。
为偶函数。
(2)
设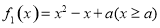 ,
,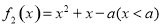
①求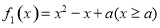 ,即
,即 的最小值:
的最小值:
若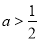 ,
,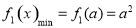 ;
;
若 ,
,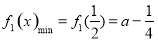
②求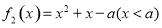 ,即
,即 的最小值
的最小值
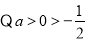 ,
,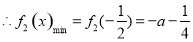
比较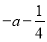 与
与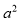 ,
,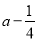 的大小:
的大小:
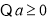
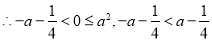 ,故
,故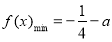
“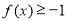 对
对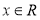 恒成立”即为“
恒成立”即为“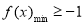 (
(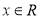 )”
)”
令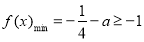 ,解得
,解得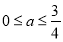 。
。
考点:奇偶性,恒成立问题

练习册系列答案
相关题目