题目内容
函数
的定义域是 （ ）
A.
B. 
C. 
D. 
D
【解析】
试题分析：由函数的解析式得
，解不等组得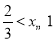
，故答案选Ｄ．
考点：1．函数的定义域；2．根式的意义；3．对数不等式的解．
练习册系列答案
相关题目
题目内容
函数的定义域是 （ ）
A. B. C. D.
D
【解析】
试题分析：由函数的解析式得，解不等组得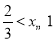，故答案选Ｄ．
考点：1．函数的定义域；2．根式的意义；3．对数不等式的解．
