题目内容

6．已知f（x）=|1-2x|，x∈[0，1]，那么方程f（f（f（x）））=$\frac{1}{2}$x的解的个数是8．

分析 化简f（f（f（x）））=|1-2|1-2|1-2x|||，作函数y=f（f（f（x）））与函数y=$\frac{1}{2}$x的图象，从而确定答案．

解答 解：∵f（x）=|1-2x|，x∈[0，1]，
∴f（f（f（x）））=|1-2|1-2|1-2x|||，
作函数y=f（f（f（x）））与函数y=$\frac{1}{2}$x的图象如下，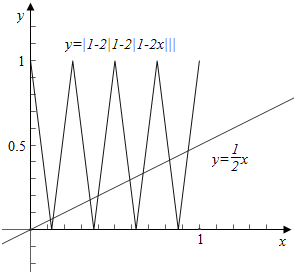

结合图象可知，
函数y=f（f（f（x）））与函数y=$\frac{1}{2}$x的图象有8个交点，
故方程f（f（f（x）））=$\frac{1}{2}$x的解的个数是8，
故答案为：8．

点评 本题考查了函数的化简与函数的图象的作法，同时考查了数形结合的思想应用．

练习册系列答案
相关题目
16．一球内切于圆锥，已知球和圆锥的底面半径分别为r，R，求圆锥的体积．
17．已知函数y=x2-2x+3在[0，m]上的最大值为3，最小值为2，求实数m的取值范围．
14．已知数列{an}的前n项和为Sn，满足an≠0，anSn+1-an+1Sn=2n-1an+1an，n∈N*．
（1）求证：Sn=2n-1an；
（2）设bn=$\frac{{a}_{n}}{{a}_{n+1}}$，求数列{bn}的前n项和Tn；
（3）对于（2）中Tn，求满足T${\;}_{{2}^{m}}$＜2013的正整数m的集合M．
1．数列{an}，Sn为前n项和，Sn=2n-1．
（1）求a${\;}_{1}^{2}$+a${\;}_{2}^{2}$+a${\;}_{3}^{2}$+…+a${\;}_{n}^{2}$；
（2）求a1+a3+…+a2n-1．
11．讨论函数f（x）=|1-x|-kx（k∈R）零点的个数．
18．已知值域为[-1，+∞）的二次函数f（x）满足f（-1+x）=f（-1-x），且方程f（x）=0两个实数根x1，x2满足|x1-x2|=2
（1）求f（x）的表达式．
（2）记max{a，b}表示a和b中的较大者，min{a，b}表示a和b中的较小者，g（x）=f（x）-kx在区间x∈[-1，2]内的最大值为max{f（2），f（-1）}，min{f（2），f（-1）}，求实数k的取值范围．
15．已知数列{an}是公比不为1的等比数列，数列{bn}满足bn=anan+1（n∈N*），试问{bn}是什么数列，为什么？
16．已知函数在定义域[-2，3]上单调递增，则满足f（2x-1）＞f（x）的x的取值范围是（　　）
A．[-2，1]B．[-2，2]C．[1，2]D．（1，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网