题目内容
15.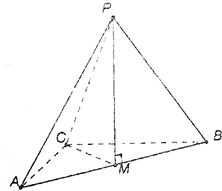 已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.
已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.(1)求证:PM⊥平面ABC;
(2)当CA=CB时,求证:CM⊥面PAB.
分析 (1)过AC取中点记作Q,连接PM,PQ,MQ,可证MQ⊥AC,PQ⊥AC,可证AC⊥面PMQ,即可得AC⊥MP,又可证MP⊥AB,即可证明MP⊥面ABC.
(2)由(1)可得PM⊥CM,由CA=CB,M为斜边AB的中点.可证CM⊥AB,即可证明CM⊥面PAB.
解答 证明:(1)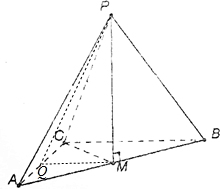 过AC取中点记作Q,
过AC取中点记作Q,
连接PM,PQ,MQ,
因为MQ∥BC(中位线),
所以MQ⊥AC,
PQ⊥AC(等腰三角形的中线即高线),
所以AC⊥面PMQ,
所以AC⊥MP,
因为MP⊥AB(等腰三角形的中线即高线),
所以MP⊥面ABC.
(2)由(1)可得PM⊥CM,
因为CA=CB,M为斜边AB的中点.
所以CM⊥AB,
又因为PM∩CM=M,
所以CM⊥面PAB.
点评 本题主要考查了直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知函数f(x)的定义域为[3,6],则函数$y=\frac{f(2x)}{{\sqrt{{{log}_{\frac{1}{2}}}(2-x)}}}$的定义域为[$\frac{3}{2},2$).
6.设α∈(0,$\frac{π}{4}$),则a=tan(sinα),b=tan(cosα)的大小关系是( )
| A. | a<b | B. | b<a | ||
| C. | a=b | D. | 不能确定,由α具体求值决定 |
4.不等式|x一2|≤5的解集为( )
| A. | [-5,5] | B. | (-2,5) | C. | [-3,7] | D. | R |