题目内容
10.已知函数f(x)定义域D={x|x≠0},且对任意的m、n∈D都有f(m•n)=f(m)+f(n).(1)求f(1)、f(-1)的值;
(2)判断f(x)的奇偶性并证明;
(3)若f(x)在(0,+∞)上是增函数,且f(4)=1,解不等式f(3x+1)+f(2x-6)≤3.
分析 (1)利用赋值法,求f(1)、f(-1)的值;
(2)结合函数奇偶性的定义即可判断函数的奇偶性;
(3)根据函数的奇偶性和单调性之间的关系将不等式进行转化即可解不等式.
解答 解:(1)∵对一切x,y∈R,都有f(m•n)=f(m)+f(n).
∴令n=1,则f(m)=f(m)+f(1),则f(1)=0,
令m=n=-1,则f(1)=f(-1)+f(-1)=0,
则f(-1)=0,
(2)令m=x,n=-1,则f(-x)=f(x)+f(-1)=f(x),
即函数f(x)是偶函数;
(3)∵f(m•n)=f(m)+f(n).
∴不等式f(3x+1)+f(2x-6)≤3.
等价为f[(3x+1)(2x-6)]≤3.
若f(4)=1,
则f(16)=f(4)+f(4)=1+1=2,
f(4)+f(16)=f(64)=1+2=3,
则f[(3x+1)(2x-6)]≤3.
等价为f[(3x+1)(2x-6)]≤f(64).
∵f(x)是偶函数且f(x)在(0,+∞)是增函数,
∴不等式等价为-64≤(3x+1)(2x-6)≤64.
即-64≤6x2-16x-6≤64.
解得-$\frac{7}{3}$≤x≤5.
点评 本题主要考查抽象函数的应用,根据函数的奇偶性和单调性的定义和性质是解决本题的关键.

练习册系列答案
相关题目
20.已知命题p:“任意的x∈R,存在m∈R,4x-2x+1-m=0且命题¬p是真命题,则实数m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<-1 | D. | m≤-1 |
1.设Sn是等差数列{an}的前n项和,若S8=S3+10,则S11=( )
| A. | 12 | B. | 18 | C. | 22 | D. | 44 |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别F1(-c,0),F2(c,0),若双曲线上存在点P,使得csin∠PF1F2=asin∠PF2F1,则该曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$] | B. | (1,$\sqrt{3}$] | C. | (1,$\sqrt{2}$+1] | D. | (1,$\sqrt{3}$+1] |
19.已知1ga+1gb=2,1ga•1gb=$\frac{1}{2}$,则|1g$\frac{a}{b}$|的值为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 1 |
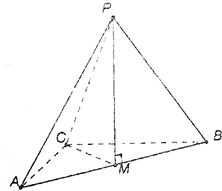 已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.
已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.