题目内容
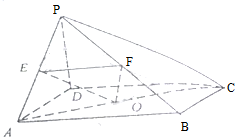
11.如图四面体P-ABC中,PA=PB=$\sqrt{13}$,平面PAB⊥平面ABC,∠ABC=90°AC=8,BC=6,则PC=7
分析 取AB中点E,连接PE,EC,证明PE⊥平面ABC,可得PE⊥CE,在直角△PEC中,可求PC的长
解答  解:取AB中点E,连接PE,EC,则
解:取AB中点E,连接PE,EC,则
∵∠ABC=90°AC=8,BC=6,
∴AB=2$\sqrt{7}$,CE=$\sqrt{43}$,
∵PA=PB=$\sqrt{13}$,E是AB中点,
∴PE=$\sqrt{6}$,PE⊥AB,
∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,
∴PE⊥平面ABC,
∵CE?平面ABC,
∴PE⊥CE,
在直角△PEC中,PC=$\sqrt{6+43}$=7,
故答案为:7.
点评 本题考查面面垂直的性质,考查线面、线线垂直,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目