题目内容
如下图,根据图中的数构成的规律,a所表示的数是( ) 
| A.12 | B.48 | C.60 | D.144 |
D
解析试题分析:观察已知三角形数阵可知其规律为每一行除首末两数外,其他数字等于其上一行两肩上的数字乘积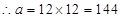
考点:归纳推理
点评:本题中首先由给定的数据得到归纳出其一般规律,再有一般规律推测 值
值

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
用反证法证明“若a,b,c<3,则a,b,c中至少有一个小于1”时,“假设”应为
| A.假设a,b,c至少有一个大于1 | B.假设a,b,c都大于1 |
| C.假设a,b,c至少有两个大于1 | D.假设a,b,c都不小于1 |
(推理)三角形的内角和为180º,凸四边形内角和为360º,那么凸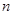 边形的内角和为
边形的内角和为
A.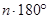 | B.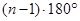 | C.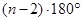 | D.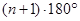 |
用反证法证明命题:若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是 ( )
中至少有一个是偶数,下列假设中正确的是 ( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个偶数 至多有一个偶数 | D.假设 至多有两个偶数 至多有两个偶数 |
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
用反证法证明命题“设a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的两根的绝对值都小于1”时,应假设
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记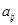 表示第
表示第 行和第
行和第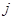 列的数,若
列的数,若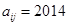 ,则
,则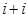 的值为( )
的值为( ) 列
列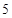 列
列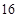
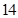

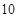
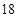

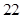
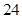
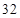

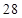
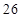
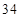
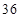
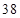
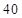
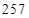 B.
B.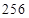 C.
C.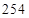 D.
D.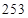
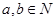 ,
,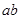 可被
可被 整除,那么
整除,那么 中至少有一个能被
中至少有一个能被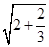 ,
,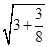 ,
,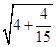 ,
,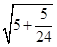 , ,由此你猜想出第n个数为
, ,由此你猜想出第n个数为