题目内容
14.与直线x+2y+4=0垂直的抛物线y=x2的切线方程是( )| A. | 2x-y+3=0 | B. | 2x-y-3=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
分析 设切点为(m,n),求出导数,求得切线的斜率,再由两直线垂直的条件可得切线的斜率,解得m=1,n=1,k=2,由点斜式方程即可得到切线方程.
解答 解:设切点为(m,n),
y=x2的导数为y′=2x,
则切线的斜率为k=2m,
由于切线与直线x+2y+4=0垂直,
则k=2m=2,
解得m=1,n=1,k=2,
即有切线的方程为y-1=2(x-1),
即为2x-y-1=0,
故选:D.
点评 本题考查导数的运用:求切线方程,主要考查导数的几何意义和两直线垂直的条件,正确求出导数和设出切点是解题的关键,属于基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
5.曲线 y=xex+2x+1在点(0,1)处的切线方程为( )
| A. | y=3x+l | B. | y=3x-l | C. | y=2x+l | D. | y=2x-l |
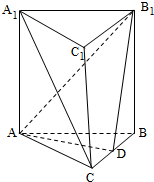 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ACB=$\frac{π}{3}$,点D是线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ACB=$\frac{π}{3}$,点D是线段BC的中点.