题目内容
【题目】已知函数f(x)=lg(![]() )(a>1>b>0).
)(a>1>b>0).
(1)求函数y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使过此两点的直线平行于x轴;
(3)当a、b满足什么关系时,f(x)在区间![]() 上恒取正值.
上恒取正值.
【答案】(1)![]() ;(2)不存在;(3)
;(2)不存在;(3)![]() .
.
【解析】
试题分析:(1)由![]()
![]()
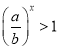 ,又
,又![]()
![]()
![]()
![]()
![]()
![]()
![]() 的定义域为
的定义域为![]() ;(2)设
;(2)设![]() ,由
,由![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 在区间
在区间![]() 上是增函数.假设函数
上是增函数.假设函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() 、
、![]() ,使得直线
,使得直线![]() 平行于
平行于![]() 轴,即
轴,即![]() ,
,![]() ,这与
,这与![]() 是增函数矛盾
是增函数矛盾![]() 函数
函数![]() 的图象上不存在不同的两点,使过此两点的直线平行于
的图象上不存在不同的两点,使过此两点的直线平行于![]() 轴;(3)由(2)知,
轴;(3)由(2)知,![]() 在区间
在区间![]() 上是增函数
上是增函数![]() 当
当![]() 时,
时,![]()
![]() 只需
只需![]()
![]()
![]()
![]()
![]()
![]()
![]() 时,
时,![]() 在区间
在区间![]() 上恒取正值.
上恒取正值.
试题解析: (1)由![]() ,得
,得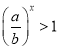 ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即函数
,即函数![]() 的定义域为
的定义域为![]() .
.
(2)设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,于是
,于是![]() ,即
,即![]() ,因此函数
,因此函数![]() 在区间
在区间![]() 上是增函数.假设函数
上是增函数.假设函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() 、
、![]() ,使得直线
,使得直线![]() 平行于
平行于![]() 轴,即
轴,即![]() ,
,![]() ,这与
,这与![]() 是增函数矛盾.故函数
是增函数矛盾.故函数![]() 的图象上不存在不同的两点,使过此两点的直线平行于
的图象上不存在不同的两点,使过此两点的直线平行于![]() 轴.
轴.
(3)由(2)知,![]() 在区间
在区间![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() ,故只需
,故只需![]() ,即
,即![]() ,即
,即![]() ,所以当
,所以当![]() 时,
时,![]() 在区间
在区间![]() 上恒取正值.
上恒取正值.

练习册系列答案
相关题目
【题目】全国人民代表大会在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作.调查发现,男、女记者中分别有10人和6人会俄语.
(1)根据以上数据完成以下![]() 列联表:
列联表:
会俄语 | 不会俄语 | 总计 | |
男 | |||
女 | |||
总计 |
(2)能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?