题目内容
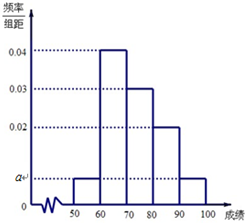 某学校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某学校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(Ⅰ)求图中a的值
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[90,100)的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
分析:(1)由频率分布直方图的性质可10(2a+0.02+0.03+0.04)=1,解方程即可得到a的值;
(2)由平均数加权公式可得平均数为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05,计算出结果既得.
(3)先求出数学成绩在[50,90)之内的人数,用100减去此数,得出结果.
(2)由平均数加权公式可得平均数为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05,计算出结果既得.
(3)先求出数学成绩在[50,90)之内的人数,用100减去此数,得出结果.
解答:解:(1)依题意,根据频率分布直方图中各个小矩形的面积和等于1得,
∴10×(2a+0.02+0.03+0.04)=1,
解得a=0.005.
∴图中a的值0.005.
(2)这100名学生语文成绩的平均分为:
55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分),
(3))数学成绩在[50,90)之内的人数为(0.005+
×0.04+
×0.03+
×0.02)×10×100=90人
数学成绩在[90,100)的人数为100-90=10人.
∴10×(2a+0.02+0.03+0.04)=1,
解得a=0.005.
∴图中a的值0.005.
(2)这100名学生语文成绩的平均分为:
55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分),
(3))数学成绩在[50,90)之内的人数为(0.005+
| 1 |
| 2 |
| 4 |
| 3 |
| 5 |
| 4 |
数学成绩在[90,100)的人数为100-90=10人.
点评:本题考查利用频率分布直方图求平均数,估计频率分别,读懂频率分布直方图,并正确的运用相关数据是解题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
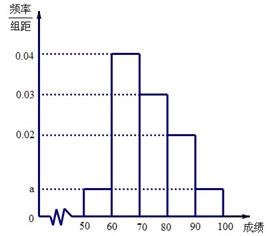 (3)若这100名学生语文成绩某些分数段的人数
(3)若这100名学生语文成绩某些分数段的人数