题目内容
已知平面几何中有勾股定理,若直角三角形ABC的两边AB、AC互相垂直,则三角形的三边长之间满足关系AB2+AC2=BC2,类比上述定理,若三棱锥S-ABC的三个侧面SAB、SAC、SBC两两互相垂直,则其面积之间有何关系 。

分析:斜边的平方等于两个直角边的平方和,可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和,边对应着面.
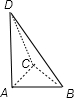
解:由边对应着面,边长对应着面积,由类比可得SBCD2=SABC2+SACD2+SADB2.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
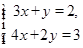 .
.  ,
,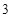 ,
,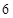 ,
,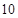 ,
,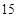 ,
,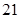 ,
,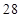 ,… 这些数叫做三角形数.则
,… 这些数叫做三角形数.则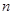 个三角形数为 ( )
个三角形数为 ( )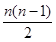
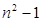
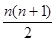

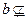 平面
平面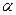 ,直线
,直线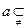 平面
平面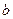 ∥平面
∥平面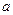 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为  中
中 中
中


 ,称为杨辉三角形,根据图中的数构成的规律,
,称为杨辉三角形,根据图中的数构成的规律, 所表示的数是
所表示的数是

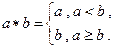 已知
已知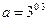 ,
, ,
, ,则
,则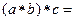 .
. ,
,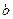 ,
,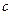 表示)
表示) ,斜边长为
,斜边长为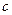 ,斜边上的高为
,斜边上的高为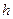 ,则有
,则有 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: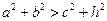 ;②
;②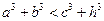 ;③
;③ 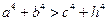 ;④
;④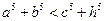 .
.