题目内容
(本题满分15分)如图,A点在x轴上方, 外接圆半径
外接圆半径 ,弦
,弦 在
在 轴上且
轴上且 轴垂直平分
轴垂直平分 边,
边,
(1)求 外接圆的标准方程
外接圆的标准方程
(2)求过点 且以
且以 为焦点的椭圆方程
为焦点的椭圆方程
(1)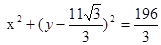 (2)
(2)
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(本题满分15分)如图,A点在x轴上方, 外接圆半径
外接圆半径 ,弦
,弦 在
在 轴上且
轴上且 轴垂直平分
轴垂直平分 边,
边,
(1)求 外接圆的标准方程
外接圆的标准方程
(2)求过点 且以
且以 为焦点的椭圆方程
为焦点的椭圆方程
(1)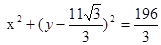 (2)
(2)
解析

 阅读快车系列答案
阅读快车系列答案