题目内容
设实数m，n，x，y满足m2+n2=3，x2+y2=4，则mx+ny的最大值为 ．
【答案】分析：根据所给的式子利用三角函数的平方关系进行换元，代入所求的式子，然后利用两角和的余弦公式进行化简，再由余弦函数的值域求出最大值．
解答：解：∵m2+n2=3，x2+y2=4，
∴设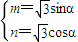
，
，
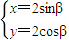∴mx+ny=2
（sinαsinβ+cosαcosβ）=2
cos（α-β），
∵-1≤cos（α-β）≤1，∴所求的最大值是2
，
故答案为：2
．
点评：本题主要考查了利用换元法求最值，利用三角函数的平方关系进行换元，再由两角和（差）的余弦公式、余弦函数的值域进行求解，属于基础题．
解答：解：∵m2+n2=3，x2+y2=4，
∴设
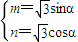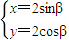，，∴mx+ny=2
（sinαsinβ+cosαcosβ）=2cos（α-β），∵-1≤cos（α-β）≤1，∴所求的最大值是2
，故答案为：2
．点评：本题主要考查了利用换元法求最值，利用三角函数的平方关系进行换元，再由两角和（差）的余弦公式、余弦函数的值域进行求解，属于基础题．
练习册系列答案
华东师大版一课一练系列答案
相关题目