题目内容
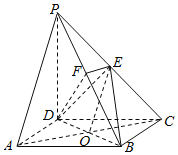
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD＝DC，点E是PC的中点，作EF⊥PB交PB于点F.
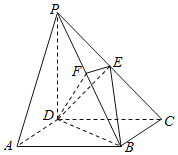
（1）求证：PA∥平面BDE；
（2）求证：PB⊥平面DEF.
【答案】（1）证明见解析；（2）证明见解析
【解析】
（1）连结AC，设AC交BD于O，连结EO，利用中位线定理以及线面平行的判定定理，即可证明；
（2）先利用线面垂直的判定定理以及线面垂直的性质得出BC⊥DE， DE⊥PB，最后利用线面垂直的判定定理得出PB⊥平面DEF.
证明：（1）连结AC，设AC交BD于O，连结EO
∵底面ABCD是矩形，∴点O是AC的中点
又∵点E是PC的中点，∴PA∥EO
∵EO平面BDE，PA平面BDE
∴PA∥平面BDE.
（2）PD⊥底面ABCD，BC底面ABCD
∴PD⊥BC
∵底面ABCD是矩形，∴CD⊥BC
∵PD∩CD＝D，PD，CD平面PDC
∴BC⊥平面PDC
∵DE平面PDC，∴BC⊥DE
∵PD＝DC，E是PC的中点，∴DE⊥PC
∵PC∩BC＝C，PC 平面PBC，BC 平面PBC
∴DE⊥平面PBC，PB平面PBC
∴DE⊥PB
又∵EF⊥PB，DE∩EF＝E，DE平面DEF，EF平面DEF
∴PB⊥平面DEF.
互动英语系列答案
名牌学校分层周周测系列答案
【题目】在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
（1）根据以上数据建立一个2×2的列联表；并估计，以运动为主的休闲方式的人的比例；
（2）能否在犯错误的概率不超过0.025的前提下，认为性别与休闲方式有关系？
附表：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2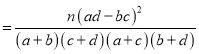
.
