题目内容
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
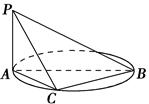
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值..

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值..
(1)见解析(2)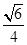
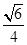
(1)由AB是圆的直径,得AC⊥BC,
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.又BC?平面PBC,
所以平面PBC⊥平面PAC.
(2)过C作CM∥AP,则CM⊥平面ABC.
如图,以点C为坐标原点,分别以直线CB,CA,CM为x轴、y轴、z轴建立空间直角坐标系.
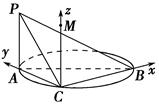
在Rt△ABC中,因为AB=2,AC=1,所以BC=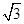 .
.
因为PA=1,所以A(0,1,0),B(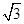 ,0,0),P(0,1,1).
,0,0),P(0,1,1).
故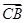 =(
=(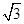 ,0,0),
,0,0),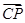 =(0,1,1).
=(0,1,1).
设平面BCP的法向量为n1=(x1,y1,z1),
则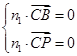 所以
所以
不妨令y1=1,则n1=(0,1,-1).
因为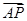 =(0,0,1),
=(0,0,1),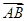 =(
=(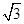 ,-1,0),
,-1,0),
设平面ABP的法向量为n2=(x2,y2,z2),
则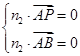 所以
所以
不妨令x2=1,则n2=(1,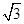 ,0).
,0).
于是cos〈n1,n2〉=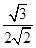 =
=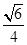 .
.
所以由题意可知二面角CPBA的余弦值为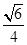
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.又BC?平面PBC,
所以平面PBC⊥平面PAC.
(2)过C作CM∥AP,则CM⊥平面ABC.
如图,以点C为坐标原点,分别以直线CB,CA,CM为x轴、y轴、z轴建立空间直角坐标系.

在Rt△ABC中,因为AB=2,AC=1,所以BC=
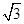 .
.因为PA=1,所以A(0,1,0),B(
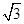 ,0,0),P(0,1,1).
,0,0),P(0,1,1).故
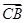 =(
=(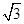 ,0,0),
,0,0),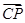 =(0,1,1).
=(0,1,1).设平面BCP的法向量为n1=(x1,y1,z1),
则
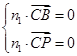 所以
所以
不妨令y1=1,则n1=(0,1,-1).
因为
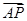 =(0,0,1),
=(0,0,1),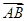 =(
=(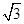 ,-1,0),
,-1,0),设平面ABP的法向量为n2=(x2,y2,z2),
则
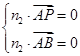 所以
所以
不妨令x2=1,则n2=(1,
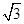 ,0).
,0).于是cos〈n1,n2〉=
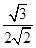 =
=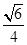 .
.所以由题意可知二面角CPBA的余弦值为
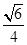

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
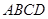 中,
中,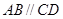 ,
,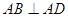 ,且
,且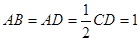 .
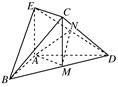
.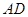 为一边向梯形外作正方形
为一边向梯形外作正方形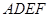 ,然后沿边
,然后沿边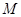 为
为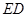 的中点,如图2.
的中点,如图2.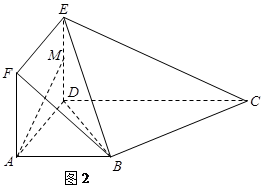
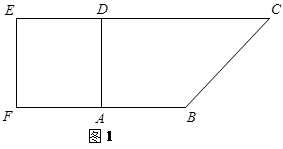
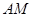 ∥平面
∥平面 ;
;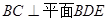 ;
;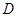 到平面
到平面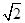 .
.
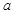 不平行于平面
不平行于平面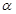 ,则下列结论成立的是( )
,则下列结论成立的是( )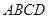 -
-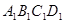 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )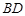 ∥
∥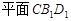
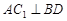
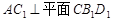
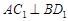
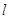 ⊥平面
⊥平面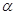 ,直线m
,直线m ,给出下列命题:
,给出下列命题: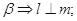 ②
②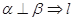 ∥m; ③
∥m; ③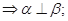 ④
④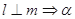 ∥
∥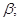 其中正确的命题是( )
其中正确的命题是( )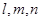 是三条互不相同的空间直线,
是三条互不相同的空间直线,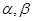 是两个不重合的平面,
是两个不重合的平面,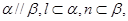 则
则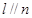 ; ②若
; ②若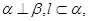 则
则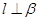 ;
;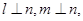 则
则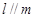 ; ④若
; ④若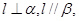 则
则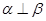
 和两个不同的平面
和两个不同的平面 ,则下列命题正确的是( )
,则下列命题正确的是( ) 则
则
 则
则
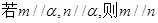
 则
则