题目内容
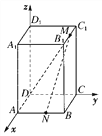
【题目】如图所示，已知正方体ABCD－A1B1C1D1的棱长为a，过点B1作B1E⊥BD1于点E，求A、E两点之间的距离.
【答案】
a
【解析】试题分析：（1）找到E点在底面上射影，即可写出E点的空间直角坐标系坐标，利用两点间距离公式可求.
试题解析：
根据题意，可得A(a,0,0)、B(a，a,0)、D1(0,0，a)、B1(a，a，a)．
过点E作EF⊥BD于F，如图所示，
则在Rt△BB1D1中，
|BB1|＝a，|BD1|＝
a，|B1D1|＝
a，
所以|B1E|＝
＝
，
所以Rt△BEB1中，|BE|＝
a
由Rt△BEF∽Rt△BD1D，得|BF|＝
a，|EF|＝
，所以点F的坐标为(
，，0)，
则点E的坐标为(，，)．
由两点间的距离公式，得
|AE|＝
＝
a，
所以A、E两点之间的距离是
a.
练习册系列答案
相关题目
