题目内容
【题目】长方体ABCD－A1B1C1D1中，AB＝BC＝2，D1D＝3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系.
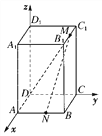
(1)写出点D、N、M的坐标；
(2)求线段MD、MN的长度．
【答案】（1）
；（2）|MD|＝
，|MN|＝
【解析】试题分析：（1）在直角坐标系中，D,N的坐标直接写出，M点坐标先找到在底面上投影的横纵坐标，再写出其坐标；（2）利用空间两点之间的距离公式求解.
试题解析：
(1)因为D是原点，则D(0,0,0)．
由AB＝BC＝2，D1D＝3，
得A(2,0,0)、B(2,2,0)、C(0,2,0)、B1(2,2,3)、C1(0,2,3)．
∵N是AB的中点，∴N(2,1,0)．
同理可得M(1,2,3)．
(2)由两点间距离公式，得
|MD|＝
＝
，
|MN|＝
＝
.
练习册系列答案
相关题目
