题目内容
16.函数f(x)=$\left\{\begin{array}{l}{{e}^{x}-1,x≥0}\\{{-x}^{2}-2x,x<0}\end{array}\right.$,若方程f[f(x)]=a(a∈R),则由该方程的实根的个数构成的集合为{1,2,3,4,5}.分析 结合分段函数可知,分三种情况讨论函数y=f[f(x)]的单调性及极值情况,从而作出函数的图象,从而确定方程f[f(x)]=a的实根个数即可.
解答 解:①当x≥0时,
f(x)=ex-1≥0且在[0,+∞)上是增函数;
故f[f(x)]在[0,+∞)上是增函数;
且f[f(x)]≥f(f(0))=0;
②当-2≤x<0时,
f(x)=-x2-2x=-(x+1)2+1,
f(x)在[-2,-1]上是增函数,在[-1,0]上是减函数;
且f(x)=-x2-2x=-(x+1)2+1≥0;
而f(x)=ex-1在[0,+∞)上是增函数;
故f[f(x)]在[-2,-1]上是增函数,在[-1,0)上是减函数;
且f(f(-2))=0,f(f(-1))=e-1,f(f(0))=0;
③当x<-2时,
f(x)=-x2-2x=-(x+1)2+1<0,
且f(x)在(-∞,-1]上是增函数,在[-1,0)上是减函数;
由-x2-2x≤-1得,
x≤-$\sqrt{2}$-1;
故f[f(x)]在(-∞,-$\sqrt{2}$-1]上是增函数,在[-$\sqrt{2}$-1,-2)上是减函数;
且f(f(-$\sqrt{2}$-1))=1,f(f(-2))=0;
作函数y=f[f(x)]的图象如下,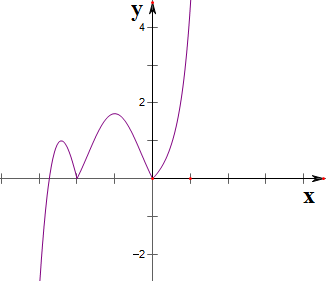
结合图象可知,
方程f[f(x)]=a解的个数可能为1,2,3,4,5;
故构成的集合为{1,2,3,4,5};
故答案为:{1,2,3,4,5}.
点评 本题考查了分段函数的应用及函数的图象与方程的根的关系应用,同时考查了分类讨论与数形结合的思想应用,属于难题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
6.函数y=$\sqrt{{{log}_{\frac{1}{2}}}(4-x)}$的定义域是( )
| A. | (-∞,4) | B. | [3,4) | C. | (3,4) | D. | [3,4] |
7.若一个2×2列联表中,由其数据计算得K2=4.013,则有95%把握认为这两个变量有关系.
参考数据:
参考数据:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
8.现有4名同学乘电梯到6至10楼去听课外知识讲座,设每名同学选择其中一个楼层下电梯的可能性相同,则乘电梯的种数是( )
| A. | 54 | B. | 45 | C. | $\frac{5×4×3×2}{2}$ | D. | 5×4×3×2 |