题目内容
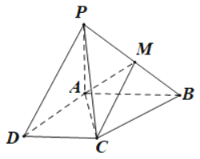
【题目】如图所示，已知四棱锥P-ABCD的底面为直角梯形，AB//DC，
，PA
底面ABCD，且PA=AD=DC=
AB=1，M是PB的中点．
（1）证明：面PAD面PCD；
（2）求AC与PB所成角的余弦值．
【答案】（1）见解析；（2）
．
【解析】
∵PA⊥AD，PA⊥AB，AD⊥AB，以A为坐标原点，AD长为长度单位，
如图建立空间直角坐标系，则各点坐标为A（0,0,0）、B（0,2,0）、C（1,1,0）、D（1,0,0）、P（0,0,1）、M（0,1,
）．
（1）证明：∵
∴
，
∴AP⊥DC．
又 由题设知AD⊥DC，且AP与AD是平面PAD内的两条相交直线，
∴DC⊥面PAD．
又∵DC
平面PCD，故面PAD⊥面PCD．
（2）解：∵
∴
∴
,
故AC与PB所成的角的余弦值为．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
