题目内容
【题目】如图是抛物线形拱桥，当水面在l时，拱顶离水面4米，水面宽8米．水位上升1米后，水面宽为（ ）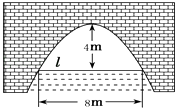 
A.
米
B.2 米
C.3 米
D.4 米
【答案】D
【解析】解：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点， 
抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半4米，抛物线顶点C坐标为（0，4），
通过以上条件可设顶点式y=ax2+4，其中a可通过代入A点坐标（﹣4，0），
到抛物线解析式得出：a=﹣ 
，所以抛物线解析式为y=﹣ x2+4，
当水面上升1米，通过抛物线在图上的观察可转化为：
当y=1时，对应的抛物线上两点之间的距离，也就是直线y=1与抛物线相交的两点之间的距离，
可以通过把y=1代入抛物线解析式得出：
1=﹣ x2+4，
解得：x=±2 
，
所以水面宽度增加到4 米，
故选：D．
练习册系列答案
相关题目
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg）．其频率分布直方图如下：
（1）设两种养殖方法的箱产量相互独立，记A表示事件：“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）．
附：
， 
