题目内容
19.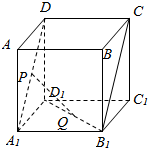 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.
设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.(1)证明:PQ∥平面AA1B1B;
(2)求异面直线PQ和B1C所成的角.
分析 (1)可连接AD,AB1,根据条件即可得出PQ为△AB1D1的中位线,从而得出PQ∥AB1,这样根据线面平行的判定定理便可得出PQ∥平面AA1B1B;
(2)根据PQ∥AB1,从而可得出∠AB1C为异面直线PQ和B1C所成的角,并容易得出∠AB1C=60°,这样即得出了异面直线PQ和B1C所成的角.
解答 解:(1)如图,连接AD,AB1;
根据条件知P,Q分别为线段AD1,D1B1的中点;
∴PQ为△AB1D1的中位线;
∴PQ∥AB1,AB1?平面AA1B1B,PQ?平面AA1B1B;
∴PQ∥平面AA1B1B;
(2)∵PQ∥AB1;
∴AB1和B1C的夹角便为异面直线PQ和B1C所成角;
即∠AB1C为异面直线PQ和B1C所成的角;
连接AC,则△ACB1为等边三角形;
∴∠AB1C=60°;
∴异面直线PQ和B1C所成的角为60°.
点评 考查正方形中心的概念,三角形中位线的性质,线面平行的判定定理,以及异面直线所成角的定义及其求法.

练习册系列答案
相关题目
7.在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1中,过点P(1,1)的弦被点P平分,则此弦所在的直线方程为( )
| A. | x+2y-3=0 | B. | x-2y-3=0 | C. | x+2y+3=0 | D. | x-2y+3=0 |
4.数列{an}中,a1∈Z,an+1=an+log2(1-$\frac{1}{n+1}$),则使{an}为整数的n的取值可能是( )
| A. | 1022 | B. | 1023 | C. | 1024 | D. | 1025 |
8.在区间(-∞,0)上单调递增的函数是( )
| A. | y=2x | B. | y=log2x | C. | y=$\frac{2}{x}$ | D. | y=-2x |
9.已知R为实数集,M=$\left\{{y\left|{y=\sqrt{1+x}}\right.}\right\}$,$N=\left\{{x|y=\sqrt{x-1}}\right\}$,则M∩(∁RN)=( )
| A. | {x|0≤x<1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤0} | D. | {x|0≤x≤1} |