题目内容
4.数列{an}中,a1∈Z,an+1=an+log2(1-$\frac{1}{n+1}$),则使{an}为整数的n的取值可能是( )| A. | 1022 | B. | 1023 | C. | 1024 | D. | 1025 |
分析 由an+1-an=log2n-log2(n+1),利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,可得an=a1-log2n,又a1∈Z,即可得出.
解答 解:∵an+1=an+log2(1-$\frac{1}{n+1}$),
∴an+1-an=log2n-log2(n+1),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(log2(n-1)-log2n)+(log2(n-2)-log2(n-1))+…+(log21-log22)+a1
=a1-log2n,
∵a1∈Z,
使{an}为整数的n的取值可能是1024.
故选:C.
点评 本题考查了递推关系的应用、“累加求和”、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.如果${log_2}\frac{1}{x}<{log_{\frac{1}{2}}}y<0$,那么( )
| A. | y<x<1 | B. | x<y<1 | C. | 1<y<x | D. | 1<x<y |
14.已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S2015的值为( )
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4030}{4031}$ |
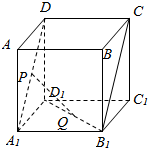 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.
设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.