题目内容
定义在R上的奇函数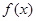 在
在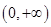 上单调递减,
上单调递减,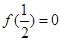 ,
,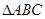 的内角A满足
的内角A满足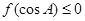 ,则A的取值范围是( )
,则A的取值范围是( )
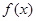 在
在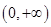 上单调递减,
上单调递减,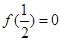 ,
,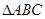 的内角A满足
的内角A满足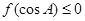 ,则A的取值范围是( )
,则A的取值范围是( )A.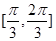 | B.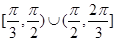 | C.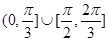 | D.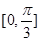 |
C
试题分析:因为f(x)是定义在R上的奇函数
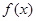 在
在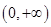 上单调递减,所以
上单调递减,所以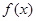 在R上都递减,由于
在R上都递减,由于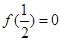 ,所以
,所以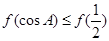 ,所以
,所以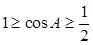 ,又因为A是三角形的内角,所以A的取值范围是
,又因为A是三角形的内角,所以A的取值范围是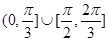 .
.
练习册系列答案
相关题目
题目内容
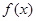 在
在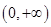 上单调递减,
上单调递减,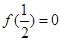 ,
,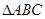 的内角A满足
的内角A满足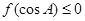 ,则A的取值范围是( )
,则A的取值范围是( )A.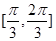 | B.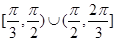 | C.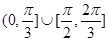 | D.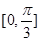 |
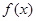 在
在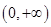 上单调递减,所以
上单调递减,所以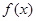 在R上都递减,由于
在R上都递减,由于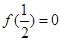 ,所以
,所以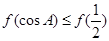 ,所以
,所以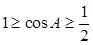 ,又因为A是三角形的内角,所以A的取值范围是
,又因为A是三角形的内角,所以A的取值范围是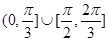 .
.