题目内容
已知函数f(x)=sin2x+
cos2x,x∈R;
(1)求f(x)的最小正周期;
(2)求f(x)在区间[0,
]上的最大值和最小值.
(3)画出函数在[0,π]上的图象.
| 3 |
(1)求f(x)的最小正周期;
(2)求f(x)在区间[0,
| π |
| 2 |
(3)画出函数在[0,π]上的图象.
f(x)=2(
sin2x+
cos2x)=2sin(2x+
).
(1)T=
=π;
(2)∵x∈[0,
],∴(2x+
)∈[
,
],
∴sin(2x+
)∈[-
,1],
∴2sin(2x+
)∈[-
,2].
∴f(x)在区间[0,
]上的最大值为-
,最小值为2.
(3)列表:
画出图象: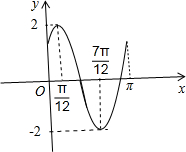
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
(1)T=
| 2π |
| 2 |
(2)∵x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴sin(2x+
| π |
| 3 |
| ||
| 2 |
∴2sin(2x+
| π |
| 3 |
| 3 |
∴f(x)在区间[0,
| π |
| 2 |
| 3 |
(3)列表:
| x | 0 |
|
|
|
| π | ||||||||||
2x+
|
|
| π |
| 2π |
| ||||||||||
sin(2x+
|
| 1 | 0 | -1 | 0 |
| ||||||||||
2sin(2x+
|
| 2 | 0 | -2 | 0 |
|


练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
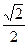 , 求
, 求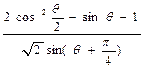 的值.
的值.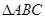 中,角
中,角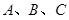 所对的边为
所对的边为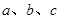 ,且满足
,且满足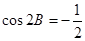 ,
,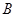 的值;(2)若
的值;(2)若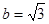 且
且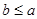 ,求
,求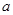 的取值范围.
的取值范围.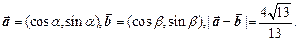
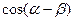 的值; (2)若
的值; (2)若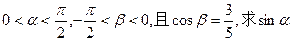 的值。
的值。