题目内容
求函数f(x)=cos
x+sin
x的图象的相邻两条对称轴之间的距离、最大值及单调减区间.
| 2 |
| 3 |
| 2 |
| 3 |
f(x)=
×(
cos
x+
sin
x)=
sin(
x+
),
∵ω=
,∴T=
=3π,
令2kπ+
≤
x+
≤2kπ+
,k∈Z,解得:3kπ+
≤x≤3kπ+
,k∈Z,
∴f(x)图象的相邻两条对称轴之间的距离为
=
,最大值为
,单调递减区间为[3kπ+
,3kπ+
],k∈Z.
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
∵ω=
| 2 |
| 3 |
| 2π |
| |ω| |
令2kπ+
| π |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
| 3π |
| 2 |
| 3π |
| 8 |
| 15π |
| 8 |
∴f(x)图象的相邻两条对称轴之间的距离为
| T |
| 2 |
| 3π |
| 2 |
| 2 |
| 3π |
| 8 |
| 15π |
| 8 |

练习册系列答案
相关题目
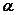 ,
,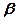 ,
,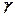 成等差数列,且公差为
成等差数列,且公差为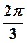 ,
,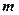 为实常数,则
为实常数,则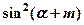 ,
,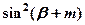 ,
,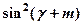 这三个三角函数式的算术平均数为____________________。
这三个三角函数式的算术平均数为____________________。
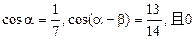 <
< <
<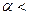
 ,
,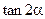 的值;
的值;
 ,则
,则 的值等于
的值等于