题目内容
【题目】如图,多面体EF﹣ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,点E在AC上的射影恰好是线段AO的中点.
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)若直线AE与平面ABCD所成的角为60°,求平面DEF与平面ABCD所成角的正弦值.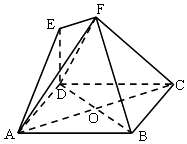
【答案】解:(Ⅰ)取AO的中点H,连结EH,则EH⊥平面ABCD
∵BD在平面ABCD内,∴EH⊥BD
又正方形ABCD中,AC⊥BD
∵EH∩AC=H,EH、AC在平面EACF内
∴BD⊥平面EACF,即BD⊥平面ACF
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,如图,以H为原点, ![]() 分别为x轴,y轴,z轴的正方向建立空间直角坐标系H﹣xyz
分别为x轴,y轴,z轴的正方向建立空间直角坐标系H﹣xyz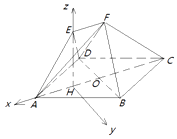
∵EH⊥平面ABCD,∴∠EAH为AE与平面ABCD所成的角,即∠EAH=60°,设正方形ABCD的边长为4a,
则AC=4 ![]() ,AH=
,AH= ![]() ,EA=2
,EA=2 ![]() ,EH=
,EH= ![]()
各点坐标分别为H(0,0,0),A( ![]() ,B(﹣
,B(﹣ ![]()
C(﹣3 ![]() ,D(﹣
,D(﹣ ![]() ,E(0,0,
,E(0,0, ![]()
易知为平面ABCD的一个法向量,记 ![]() ,
,![]() ,
, ![]() ,
,
∵EF∥AC,∴ ![]()
设平面DEF的一个法向量为 ![]() ,则
,则 ![]() ⊥
⊥ ![]() ,
, ![]()
![]() ⊥,
⊥,
即 ![]() ,令z=
,令z= ![]() ,则x=0,y=﹣2,∴
,则x=0,y=﹣2,∴ ![]() ,且
,且 ![]() ,
,
∴ ![]() 与
与 ![]() 的夹角θ为|cosθ|=
的夹角θ为|cosθ|= ![]()
平面DEF与平面ABCD所成角α的正弦值为sinα= ![]()
【解析】(Ⅰ)取AO的中点H,连结EH,只需证EH⊥BD,AC⊥BD,即可得BD⊥平面ACF(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,如图,以H为原点, ![]() 分别为x轴,y轴,z轴的正方向建立空间直角坐标系H﹣xyz,求出两个面的法向量,利用向量的夹角公式即可求解.
分别为x轴,y轴,z轴的正方向建立空间直角坐标系H﹣xyz,求出两个面的法向量,利用向量的夹角公式即可求解.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】某综艺节目为增强娱乐性,要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会;凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动,以此下去.
(Ⅰ)假设每个人选择表演与否是等可能的,且互不影响,则某人选择表演后,其连线的3个好友中不少于2个好友选择表演节目的概率是多少?
(Ⅱ)为调查“选择表演者”与其性别是否有关,采取随机抽样得到如表:
选择表演 | 拒绝表演 | 合计 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合计 | 60 | 20 | 80 |
①根据表中数据,是否有99%的把握认为“表演节目”与好友的性别有关?
②将此样本的频率视为总体的概率,随机调查3名男性好友,设X为3个人中选择表演的人数,求X的分布列和期望.
附:K2= ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |

