题目内容
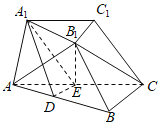
【题目】如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,AB=2A1B1,B1E⊥平面ABC,且∠ACB=90°.
(Ⅰ)求证:B1C∥平面A1DE;
(Ⅱ)若AC=3BC=6,△AB1C为等边三角形,求四棱锥A1﹣B1C1ED的体积.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取D,E分别是AB,AC的中点,易证得平面A1DE∥平面B1BC,从而可证得B1C∥平面A1DE;
(Ⅱ)利用![]() =
=![]() -
-![]() ,分别由柱体和椎体体积公式求解即可.
,分别由柱体和椎体体积公式求解即可.
(Ⅰ)证明:因为在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,AB=2A1B1,
所以DE∥BC,A1B1∥BD,A1B1=BD,
所以四边形DBB1A1是平行四边形,所以A1D∥BB1,
因为A1D∩DE=D,BB1∩BC=B,
A1D、DE平面A1DE,BB1、BC平面BCB1,
所以平面A1DE∥平面B1BC,
所以B1C平面B1BC,所以B1C∥平面A1DE.
(Ⅱ)因为AC=3BC=6,△AB1C为等边三角形,
AB=2A1B1,B1E⊥平面ABC,且∠ACB=90°.
所以AE=3,DE=1,B1E=![]() =
=![]() ,∠AED=90°,
,∠AED=90°,
所以四棱锥A1﹣B1C1ED的体积:![]() =
=![]() -
-![]()
=![]() ﹣
﹣![]() =
=![]() =
=![]()
=![]() =
=![]() .
.

【题目】根据历年市场行情,某种农产品在4月份的30天内每吨的售价p(万元)与时间t(天)![]() 的关系如图的折线表示.又知该农产品在30天内的日交易量Q(吨)与时间t(天)满足一次函数关系,部分数据如表所示.
的关系如图的折线表示.又知该农产品在30天内的日交易量Q(吨)与时间t(天)满足一次函数关系,部分数据如表所示.

第t天 | 4 | 10 | 16 | 22 |
Q(吨) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,求出该种农产品每吨的售价p(万元)与时间t(天)所满足的函数关系式;
(2)若该农产品日交易额![]() 每吨的售价
每吨的售价![]() 日交易量,求在这30天中,该农产品日交易额y(万元)的最大值.
日交易量,求在这30天中,该农产品日交易额y(万元)的最大值.
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年科研费用和年利润具体数据如下表:
(百万元)之间具有线性相关关系,近5年的年科研费用和年利润具体数据如下表:
年科研费用 | 1 | 2 | 3 | 4 | 5 |
企业所获利润 | 2 | 3 | 4 | 4 | 7 |
(1)画出散点图;
(2)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(3)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考公式:用最小二乘法求回归方程![]() 的系数
的系数![]() 计算公式:
计算公式:

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:
(单位:![]() )的影响,对近
)的影响,对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量
和年销售量![]() 作了初步统计和处理,得到的数据如下:
作了初步统计和处理,得到的数据如下:
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
![]() ,
,![]() .
.

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若公司计划下一年度投入宣传费![]() 万元,试预测年销售量
万元,试预测年销售量![]() 的值.
的值.
参考公式


